
Actualmente con el boom de la Big Data, tener nociones de probabilidad y estadística se ha hecho fundamental. En los últimos años ha habido un resurgimiento de todo lo relacionado con estadística , data mining y machine learning empujados principalmente por la explosión de datos con que contamos, estos conceptos combinados forman la base de lo que actualmente se conoce como la Ciencia de Datos. Dentro de este contexto, Python es uno de los lenguajes que más nos facilita trabajar con datos. Realizar complejos análisis estadísticos nunca fue tan fácil como con Python!
¿Qué es la Estadística?¶
La estadística suele ser definida como la ciencia de aprender de los datos o como la ciencia de obtener conclusiones en la presencia de incertidumbre. Se relaciona principalmente con la recolección, análisis e interpretación de datos, así como también con la efectiva comunicación y presentación de los resultados basados en esos datos. Como por datos entendemos a cualquier clase de información grabada, la estadística juego un rol importante en muchas disciplinas científicas.
La estadística puede ser muy importante para una efectiva toma de decisiones. Existe una gran cantidad de valiosa información escondida entre los datos, pero esta información no suele ser fácilmente accesible, la estadística nos brinda los principios fundamentales que nos permiten extraer y entender esa información; tambien nos proporciona las herramientas necesarias para verificar la calidad de nuestros datos y nuestra información.
La estadística suele ser dividida en dos grandes ramas:
La estadística descriptiva: La cual se dedica a recolectar, ordenar, analizar y representar a un conjunto de datos, con el fin de describir apropiadamente las características de este. Calcula los parámetros estadísticos que describen el conjunto estudiado. Algunas de las herramientas que utiliza son gráficos, medidas de frecuencias, medidas de centralización, medidas de posición, medidas de dispersión, entre otras.
La estadistica inferencial: La cual estudia cómo sacar conclusiones generales para toda la población a partir del estudio de una muestra, y el grado de fiabilidad o significación de los resultados obtenidos. Sus principales herramientas son el muestreo, la estimación de parámetros y el contraste de hipótesis.
¿Qué es la Probabilidad?¶
La probabilidad mide la mayor o menor posibilidad de que se dé un determinado resultado (suceso o evento) cuando se realiza un experimento aleatorio. Para calcular la probabilidad de un evento se toma en cuenta todos los casos posibles de ocurrencia del mismo; es decir, de cuántas formas puede ocurrir determinada situación.Los casos favorables de ocurrencia de un evento serán los que cumplan con la condición que estamos buscando. La probabilidad toma valores entre 0 y 1 (o expresados en tanto por ciento, entre 0% y 100%).
La probabilidad es a la vez el inverso y complemento para la estadística. Dónde la estadística nos ayuda a ir desde los datos observados hasta hacer generalizaciones sobre como funcionan las cosas; la probabilidad funciona en la dirección inversa: si asumimos que sabemos como las cosas funcionan, entonces podemos averiguar la clase de datos que vamos a ver y cuan probable es que los veamos.
La probabilidad también funciona como complemento de la estadística cuando nos proporciona una sólida base para la estadistica inferencial. Cuando hay incertidumbre, no sabemos que puede pasar y hay alguna posibilidad de errores, utilizando probabilidades podemos aprender formas de controlar la tasa de errores para reducirlos.
Actividades básicas del analisis estadístico¶
Las técnicas estadísticas deberían ser vistas como una parte importante de cualquier proceso de toma de dicisiones, permitiendo tomar decisiones estratégicamente informadas que combinen intuición con experiencia y un entendimiento estadístico de los datos que tenemos disponibles.
Un análisis estadístico suele contener 5 actividades básicas:
Diseño del análisis: Esta actividad involucra el planeamiento de los detalles para obtener los datos que necesitamos y la generación de la hipótesis a ser evaluada.
Exploración de datos: En esta actividad nos dedicamos a jugar con nuestros datos, los describimos, los resumimos, realizamos gráficos para mirarlos desde distintos ángulos. Esta exploración nos ayuda a asegurarnos que los datos que obtuvimos son completos y que la etapa de diseño fue correcta.
Armado del modelo: En esta actividad intentamos armar un modelo que explique el comportamiento de nuestros datos y pueda llegar a hacer predicciones sobre los mismos. La idea es que el modelo pueda describir las propiedades fundamentales de nuestros datos.
Realizar estimaciones: Aquí vamos a intentar realizar estimaciones basadas en el modelo que armamos anteriormente. También vamos a intentar estimar el tamaño del error que nuestro modelo puede tener en sus predicciones.
Contraste de la hipótesis: Esta actividad es la que va a producir la decisión final sobre si las predicciones del modelo son correctas y ayudarnos a concluir si los datos que poseemos confirman o rechazan la hipótesis que generamos en la actividad 1.
Conceptos básicos de la estadística descriptiva¶
En estadística descriptiva se utilizan distintas medidas para intentar describir las propiedades de nuestros datos, algunos de los conceptos básicos, son:
- Media aritmética: La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total elementos. Se suele representar con la letra griega $\mu$. Si tenemos una muestra de $n$ valores, $x_i$, la media aritmética, $\mu$, es la suma de los valores divididos por el numero de elementos; en otras palabras: $$\mu = \frac{1}{n} \sum_{i}x_i$$
- Desviación respecto a la media: La desviación respecto a la media es la diferencia en valor absoluto entre cada valor de la variable estadística y la media aritmética. $$D_i = |x_i - \mu|$$
- Varianza: La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística. La varianza intenta describir la dispersión de los datos. Se representa como $\sigma^2$. $$\sigma^2 = \frac{\sum\limits_{i=1}^n(x_i - \mu)^2}{n} $$
- Desviación típica: La desviación típica es la raíz cuadrada de la varianza. Se representa con la letra griega $\sigma$. $$\sigma = \sqrt{\frac{\sum\limits_{i=1}^n(x_i - \mu)^2}{n}} $$
- Moda: La moda es el valor que tiene mayor frecuencia absoluta. Se representa con $M_0$
- Mediana: La mediana es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. Se representa con $\widetilde{x}$.
- Correlación: La correlación trata de establecer la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional. Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra. En caso de que suceda, diremos que las variables están correlacionadas o que hay correlación entre ellas. La correlación es positiva cuando los valores de las variables aumenta juntos; y es negativa cuando un valor de una variable se reduce cuando el valor de la otra variable aumenta.
- Covarianza: La covarianza es el equivalente de la varianza aplicado a una variable bidimensional. Es la media aritmética de los productos de las desviaciones de cada una de las variables respecto a sus medias respectivas.La covarianza indica el sentido de la correlación entre las variables; Si $\sigma_{xy} > 0$ la correlación es directa; Si $\sigma_{xy} < 0$ la correlación es inversa.
- Valor atípico: Un valor atípico es una observación que se aleja demasiado de la moda; esta muy lejos de la tendencia principal del resto de los datos. Pueden ser causados por errores en la recolección de datos o medidas inusuales. Generalmente se recomienda eliminarlos del conjunto de datos.
Librerías de Python para probabilidad y estadística¶
Como ya les vengo mostrando en mis anteriores artículos, Python se lleva muy bien con las matemáticas. Además, la comunidad python es tan amplia que solemos encontrar una librería para cualquier problema al que nos enfrentemos. En este caso, los principales módulos que Python nos ofrece para trabajar con probabilidad y estadística, son:
numpy: El popular paquete matemático de Python, se utiliza tanto que mucha gente ya lo considera parte integral del lenguaje. Nos proporciona algunas funciones estadísticas que podemos aplicar fácilmente sobre los arrays de Numpy.
scipy.stats: Este submodulo del paquete científico Scipy es el complemento perfecto para Numpy, las funciones estadisticas que no encontremos en uno, las podemos encontrar en el otro.
statsmodels: Esta librería nos brinda un gran número de herramientas para explorar datos, estimar modelos estadísticos, realizar pruebas estadísticas y muchas cosas más.
matplotlib: Es la librería más popular en Python para visualizaciones y gráficos. Ella nos va a permitir realizar los gráficos de las distintas distribuciones de datos.
seaborn: Esta librería es un complemento ideal de matplotlib para realizar gráficos estadísticos.
pandas: Esta es la librería más popular para análisis de datos y financieros. Posee algunas funciones muy útiles para realizar estadística descriptiva sobre nuestros datos y nos facilita sobremanera el trabajar con series de tiempo.
pyMC: pyMC es un módulo de Python que implementa modelos estadísticos bayesianos, incluyendo la cadena de Markov Monte Carlo(MCMC). pyMC ofrece funcionalidades para hacer el análisis bayesiano lo mas simple posible.
Ejemplos en Python¶
Calcular los principales indicadores de la estadística descriptiva con Python es muy fácil!.
# Ejemplos de estadistica descriptiva con python
import numpy as np # importando numpy
from scipy import stats # importando scipy.stats
import pandas as pd # importando pandas
np.random.seed(2131982) # para poder replicar el random
datos = np.random.randn(5, 4) # datos normalmente distribuidos
datos
# media arítmetica
datos.mean() # Calcula la media aritmetica de
np.mean(datos) # Mismo resultado desde la funcion de numpy
datos.mean(axis=1) # media aritmetica de cada fila
datos.mean(axis=0) # media aritmetica de cada columna
# mediana
np.median(datos)
np.median(datos, 0) # media aritmetica de cada columna
# Desviación típica
np.std(datos)
np.std(datos, 0) # Desviación típica de cada columna
# varianza
np.var(datos)
np.var(datos, 0) # varianza de cada columna
# moda
stats.mode(datos) # Calcula la moda de cada columna
# el 2do array devuelve la frecuencia.
datos2 = np.array([1, 2, 3, 6, 6, 1, 2, 4, 2, 2, 6, 6, 8, 10, 6])
stats.mode(datos2) # aqui la moda es el 6 porque aparece 5 veces en el vector.
# correlacion
np.corrcoef(datos) # Crea matriz de correlación.
# calculando la correlación entre dos vectores.
np.corrcoef(datos[0], datos[1])
# covarianza
np.cov(datos) # calcula matriz de covarianza
# covarianza de dos vectores
np.cov(datos[0], datos[1])
# usando pandas
dataframe = pd.DataFrame(datos, index=['a', 'b', 'c', 'd', 'e'],
columns=['col1', 'col2', 'col3', 'col4'])
dataframe
# resumen estadistadistico con pandas
dataframe.describe()
# sumando las columnas
dataframe.sum()
# sumando filas
dataframe.sum(axis=1)
dataframe.cumsum() # acumulados
# media aritmetica de cada columna con pandas
dataframe.mean()
# media aritmetica de cada fila con pandas
dataframe.mean(axis=1)
Histogramas y Distribuciones¶
Muchas veces los indicadores de la estadística descriptiva no nos proporcionan una imagen clara de nuestros datos. Por esta razón, siempre es útil complementarlos con gráficos de las distribuciones de los datos, que describan con qué frecuencia aparece cada valor. La representación más común de una distribución es un histograma, que es un gráfico que muestra la frecuencia o probabilidad de cada valor. El histograma muestra las frecuencias como un gráfico de barras que indica cuan frecuente un determinado valor ocurre en el conjunto de datos. El eje horizontal representa los valores del conjunto de datos y el eje vertical representa la frecuencia con que esos valores ocurren.
Las distribuciones se pueden clasificar en dos grandes grupos:
Las distribuciones continuas, que son aquellas que presentan un número infinito de posibles soluciones. Dentro de este grupo vamos a encontrar a las distribuciones:
- normal,
- gamma,
- chi cuadrado,
- t de Student,
- pareto,
- entre otras
Las distribuciones discretas, que son aquellas en las que la variable puede tomar un número determinado de valores. Los principales exponentes de este grupo son las distribuciones:
- poisson,
- binomial,
- hipergeométrica,
- bernoulli
- entre otras
Veamos algunos ejemplos graficados con la ayuda de Python.
Distribución normal¶
La distribución normal es una de las principales distribuciones, ya que es la que con más frecuencia aparece aproximada en los fenómenos reales. Tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Con la ayuda de Python la podemos graficar de la siguiente manera:
# Graficos embebidos.
%matplotlib inline
import matplotlib.pyplot as plt # importando matplotlib
import seaborn as sns # importando seaborn
# parametros esteticos de seaborn
sns.set_palette("deep", desat=.6)
sns.set_context(rc={"figure.figsize": (8, 4)})
mu, sigma = 0, 0.1 # media y desvio estandar
s = np.random.normal(mu, sigma, 1000) #creando muestra de datos
# histograma de distribución normal.
cuenta, cajas, ignorar = plt.hist(s, 30, normed=True)
normal = plt.plot(cajas, 1/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (cajas - mu)**2 / (2 * sigma**2) ),
linewidth=2, color='r')
Distribuciones simetricas y asimetricas¶
Una distribución es simétrica cuando moda, mediana y media coinciden aproximadamente en sus valores. Si una distribución es simétrica, existe el mismo número de valores a la derecha que a la izquierda de la media, por tanto, el mismo número de desviaciones con signo positivo que con signo negativo.
Una distribución tiene asimetria positiva (o a la derecha) si la "cola" a la derecha de la media es más larga que la de la izquierda, es decir, si hay valores más separados de la media a la derecha. De la misma forma una distribución tiene asimetria negativa (o a la izquierda) si la "cola" a la izquierda de la media es más larga que la de la derecha, es decir, si hay valores más separados de la media a la izquierda.
Las distribuciones asimétricas suelen ser problemáticas, ya que la mayoría de los métodos estadísticos suelen estar desarrollados para distribuciones del tipo normal. Para salvar estos problemas se suelen realizar transformaciones a los datos para hacer a estas distribuciones más simétricas y acercarse a la distribución normal.
# Dibujando la distribucion Gamma
x = stats.gamma(3).rvs(5000)
gamma = plt.hist(x, 70, histtype="stepfilled", alpha=.7)
En este ejemplo podemos ver que la distribución gamma que dibujamos tiene una asimetria positiva.
# Calculando la simetria con scipy
stats.skew(x)
Cuartiles y diagramas de cajas¶
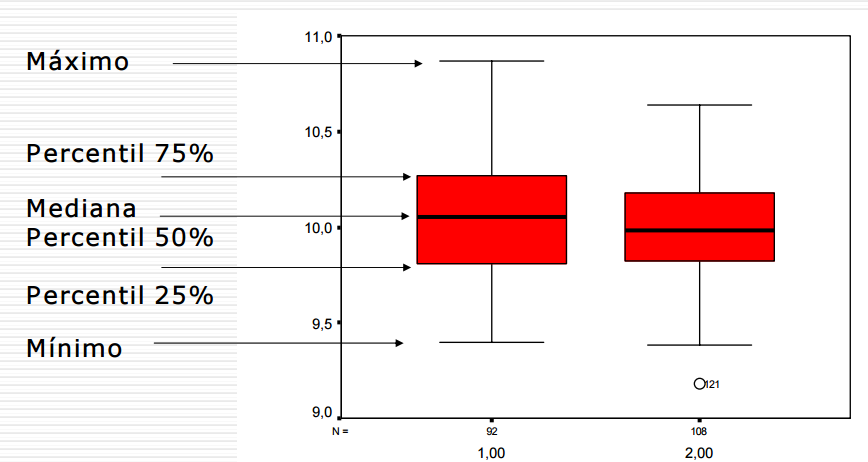
Los cuartiles son los tres valores de la variable estadística que dividen a un conjunto de datos ordenados en cuatro partes iguales. Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al 75% de los datos. Q2 coincide con la mediana.
Los diagramas de cajas son una presentación visual que describe varias características importantes al mismo tiempo, tales como la dispersión y simetría. Para su realización se representan los tres cuartiles y los valores mínimo y máximo de los datos, sobre un rectángulo, alineado horizontal o verticalmente. Estos gráficos nos proporcionan abundante información y son sumamente útiles para encontrar valores atípicos y comparar dos conjunto de datos.
# Ejemplo de grafico de cajas en python
datos_1 = np.random.normal(100, 10, 200)
datos_2 = np.random.normal(80, 30, 200)
datos_3 = np.random.normal(90, 20, 200)
datos_4 = np.random.normal(70, 25, 200)
datos_graf = [datos_1, datos_2, datos_3, datos_4]
# Creando el objeto figura
fig = plt.figure(1, figsize=(9, 6))
# Creando el subgrafico
ax = fig.add_subplot(111)
# creando el grafico de cajas
bp = ax.boxplot(datos_graf)
# visualizar mas facile los atípicos
for flier in bp['fliers']:
flier.set(marker='o', color='red', alpha=0.5)
# los puntos aislados son valores atípicos
# usando seaborn
sns.boxplot(datos_graf, names=["grupo1", "grupo2", "grupo3", "grupo 4"],
color="PaleGreen");
Regresiones¶
Las regresiones es una de las herramientas principales de la estadistica inferencial. El objetivo del análisis de regresión es describir la relación entre un conjunto de variables, llamadas variables dependientes, y otro conjunto de variables, llamadas variables independientes o explicativas. Más específicamente, el análisis de regresión ayuda a entender cómo el valor típico de la variable dependiente cambia cuando cualquiera de las variables independientes es cambiada, mientras que se mantienen las otras variables independientes fijas. El producto final del análisis de regresión es la estimación de una función de las variables independientes llamada la función de regresión. La idea es que en base a esta función de regresión podamos hacer estimaciones sobre eventos futuros.
La regresión lineal es una de las técnicas más simples y mayormente utilizadas en los análisis de regresiones. Hace suposiciones muy rígidas sobre la relación entre la variable dependiente $y$ y variable independiente $x$. Asume que la relación va a tomar la forma:
$$ y = \beta_0 + \beta_1 * x$$Uno de los métodos más populares para realizar regresiones lineales es el de mínimos cuadrados ordinarios (OLS, por sus siglas en inglés), este método es el estimador más simple y común en la que los dos $\beta$s se eligen para minimizar el cuadrado de la distancia entre los valores estimados y los valores reales.
Realizar análisis de regresiones en Python es sumamente fácil gracias a statsmodels.
Veamos un pequeño ejemplo utilizando el dataset longley, el cual es ideal para realizar regresiones:
# importanto la api de statsmodels
import statsmodels.formula.api as smf
import statsmodels.api as sm
# Creando un DataFrame de pandas.
df = pd.read_csv('https://vincentarelbundock.github.io/Rdatasets/csv/datasets/longley.csv', index_col=0)
df.head() # longley dataset
# utilizando la api de formula de statsmodels
est = smf.ols(formula='Employed ~ GNP', data=df).fit()
est.summary() # Employed se estima en base a GNP.
Como podemos ver, el resumen que nos brinda statsmodels sobre nuestro modelo de regresión contiene bastante información sobre como se ajuste el modelo a los datos. Pasemos a explicar algunos de estos valores:
- Dep. Variable: es la variable que estamos estimasdo.
- Model: es el modelo que estamos utilizando.
- R-squared: es el coeficiente de determinación, el cual mide cuan bien nuestra recta de regresion se aproxima a los datos reales.
- Adj. R-squared: es el coeficiente anterior ajustado según el número de observaciones.
- [95.0% Conf. Int.]: Los valores inferior y superior del intervalo de confianza del 95%.
- coef: el valor estimado del coeficiente.
- std err: el error estándar de la estimación del coeficiente.
- Skew: una medida de la asimetria de los datos sobre la media.
- Kurtosis: Una medida de la forma de la distribución. La curtosis compara la cantidad de datos cerca de la media con los que están más lejos de la media(en las colas).
# grafico de regresion. que tanto se ajusta el modelo a los datos.
y = df.Employed # Respuesta
X = df.GNP # Predictor
X = sm.add_constant(X) # agrega constante
X_1 = pd.DataFrame({'GNP': np.linspace(X.GNP.min(), X.GNP.max(), 100)})
X_1 = sm.add_constant(X_1)
y_reg = est.predict(X_1) # estimacion
plt.scatter(X.GNP, y, alpha=0.3) # grafica los puntos de datos
plt.ylim(30, 100) # limite de eje y
plt.xlabel("Producto bruto") # leyenda eje x
plt.ylabel("Empleo") # leyenda eje y
plt.title("Ajuste de regresion") # titulo del grafico
reg = plt.plot(X_1.GNP, y_reg, 'r', alpha=0.9) # linea de regresion
# grafico de influencia
from statsmodels.graphics.regressionplots import influence_plot
inf =influence_plot(est)
Este último gráfico nos muestra el apalancamiento y la influencia de cada caso.
La estadística bayesiana¶
La estadística bayesiana es un subconjunto del campo de la estadística en la que la evidencia sobre el verdadero estado de las cosas se expresa en términos de grados de creencia. Esta filosofía de tratar a las creencias como probabilidad es algo natural para los seres humanos. Nosotros la utilizamos constantemente a medida que interactuamos con el mundo y sólo vemos verdades parciales; necesitando reunir pruebas para formar nuestras creencias.
La diferencia fundamental entre la estadística clásica (frecuentista) y la bayesiana es el concepto de probabilidad. Para la estadística clásica es un concepto objetivo, que se encuentra en la naturaleza, mientras que para la estadística bayesiana se encuentra en el observador, siendo así un concepto subjetivo. De este modo, en estadística clásica solo se toma como fuente de información las muestras obtenidas. En el caso bayesiano, sin embargo, además de la muestra también juega un papel fundamental la información previa o externa que se posee en relación a los fenómenos que se tratan de modelar.
La estadística bayesiana está demostrando su utilidad en ciertas estimaciones basadas en el conocimiento subjetivo a priori y el hecho de permitir revisar esas estimaciones en función de la evidencia empírica es lo que está abriendo nuevas formas de hacer conocimiento. Una aplicación de esto son los clasificadores bayesianos que son frecuentemente usados en implementaciones de filtros de correo basura, que se adaptan con el uso. La estadística bayesiana es un tema muy interesante que merece un artículo en sí mismo.
Para entender más fácilmente como funciona la estadística bayesiana veamos un simple ejemplo del lanzamiento de una moneda. La idea principal de la inferencia bayesiana es que la noción de probabilidad cambia mientras más datos tengamos.
sns.set_context(rc={"figure.figsize": (11, 9)})
dist = stats.beta
n_trials = [0, 1, 2, 3, 4, 5, 8, 15, 50, 500]
data = stats.bernoulli.rvs(0.5, size=n_trials[-1])
x = np.linspace(0, 1, 100)
for k, N in enumerate(n_trials):
sx = plt.subplot(len(n_trials) / 2, 2, k + 1)
plt.xlabel("$p$, probabilidad de cara") \
if k in [0, len(n_trials) - 1] else None
plt.setp(sx.get_yticklabels(), visible=False)
heads = data[:N].sum()
y = dist.pdf(x, 1 + heads, 1 + N - heads)
plt.plot(x, y, label="lanzamientos observados %d,\n %d caras" % (N, heads))
plt.fill_between(x, 0, y, color="#348ABD", alpha=0.4)
plt.vlines(0.5, 0, 4, color="k", linestyles="--", lw=1)
leg = plt.legend()
leg.get_frame().set_alpha(0.4)
plt.autoscale(tight=True)
plt.suptitle("Actualizacion Bayesiana de probabilidades posterios",
y=1.02,
fontsize=14)
plt.tight_layout()
Como el gráfico de arriba muestra, cuando empezamos a observar nuevos datos nuestras probabilidades posteriores comienzan a cambiar y moverse. Eventualmente, a medida que observamos más y más datos (lanzamientos de monedas), nuestras probabilidades se acercan más y más hacia el verdadero valor de p = 0.5 (marcado por una línea discontinua).