
Introducción¶
El artículo de hoy se lo voy a dedicar a uno los números más fascinantes de las Matemáticas, el número $e$. Este número es de suma importancia, ya que lo podemos encontrar en una gran variedad de fenómenos, desde Física y Biología, hasta Finanzas, Arte y Música. Así como el famoso $\pi$, gobierna el círculo, $e$ gobierna el Cálculo y los Logaritmos.
¿Qué es el número $e$?¶
El número $e$ es una de las más importantes constantes matemáticas, pertenece al grupo de los números irracionales, es decir, que el mismo no puede ser expresado como una fracción de dos números enteros y su expansión decimal es infinita. Asimismo, también es un número trascendental, lo que quiere decir que tampoco puede ser expresado algebraicamente. Sus primeros dígitos son:
$$e = 2.7182818284590452353602874713527\dots$$Otra cosa que hace a $e$ sumamente interesante, es que es la base del Logaritmo natural, es decir que si $\ln(x) = y$, entonces $e^y = x$. También podemos encontrar a $e$, en la función exponencial, $e^x$, la cual es la inversa de la función del Logaritmo natural, y tiene la particularidad de que la derivada de $e^x$, es la misma función $e^x$. Esta característica, es lo que que hace a $e$ fundamental para el Cálculo.
Historia del número $e$¶
Para poder entender más en profundidad la naturaleza del número $e$, debemos recorrer un poco de su historia, que a diferencia de $\pi$, que tiene una historia milenaria, es relativamente reciente.
Invención del Logaritmo¶
La historia del número $e$ comienza en el siglo XVII, cuando John Napier inventó el concepto de Logaritmo. Pocas veces en la historia de la ciencia, un concepto matemático fue recibido con tanto entusiasmo por la comunidad científica, como fue el caso del Logaritmo. La idea básica detrás de este concepto abstracto es la siguiente: Si uno pudiera escribir cualquier número positivo como la potencia de otro número fijo (llamado base), entonces la multiplicación y la división de números pasaría a ser equivalente a sumar o restar sus potencias; lo que simplificaría y facilitaría los cálculos. Para entenderlo mejor, veamos un ejemplo, supongamos que tenemos la siguiente tabla de potencias de 2.
| $n$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $2^n$ | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
Ahora si quisiéramos saber el resultado de multiplicar 32 por 64; simplemente deberíamos buscar las potencias de estos dos números en la tabla anterior, 5 para 32 y 6 para 64, luego sumamos estos dos números, los que nos da como resultado 11 y por último si vamos a buscar el resultado de elevar 2 a la 11 potencia en la misma tabla, encontramos el resultado de nuestra multiplicación, que es 2048. Utilizando una simple tabla de Logaritmos, se podían resolver multiplicaciones y divisiones complejas en segundos, algo muy útil en el siglo XVII, dónde no existían las calculadoras!.
Si bien John Napier desarrollo el concepto de Logaritmo, el mismo difiere un poco del concepto moderno que tenemos hoy en día; y tampoco fue el responsable de notar el poder $e$ como base de los mismos. Tendríamos que esperar algunos años más hasta que $e$ se apoderara por completo de los Logaritmos, como la base más natural para ellos. Veamos el camino que hubo que recorrer.
El área de la hipérbola¶
Un problema muy común en Matemáticas, es el de encontrar el área de una figura plana, este proceso se conoce con el nombre de cuadratura o integración. Desde que los matemáticos comenzaron a trabajar en estos problemas, una de las figuras que más ha resistido obstinadamente todos los intentos de cuadratura era la hipérbola, la cual esta definida por la función $f(x) = \frac{1}{x}$.
Un matemático que se interesó por un tema muy cercano a este, también en el siglo XVII, fue Pierre de Fermat. Fermat se interesó en la cuadratura de curvas cuya función general tiene la forma $f(x) = x^n$, dónde $n$ es un número entero. Estas curvas son llamadas generalmente parábolas. Utilizando el método de exhaución, el cuál explique en mi artículo anterior, Fermat fue capaz de llegar a una fórmula general para encontrar el área de esta familia de curvas. La fórmula a la que arribó fue la siguiente:
$$A = \frac{a^{n + 1}}{n + 1}$$Como podemos ver, esta no es ni más ni menos que la regla de integración para funciones de grado $n$.
$$\int x^{n} \ dx = \frac{x^{n + 1}}{n + 1}$$Debemos recordar, sin embargo, que el trabajo de Fermat fue hecho alrededor de 1640, aproximadamente unos 30 años antes de que Newton y Leibniz establecieran esta fórmula como parte del cálculo integral. A pesar de que Fermat pudo probar que su fórmula podía ser aplicada tanto para los casos de $n$ siendo un entero positivo como negativo; hubo un caso que se le siguió escapando, el caso de $n = -1$, es decir el caso del área de la hipérbola, $f(x) = \frac{1}{x}$; ya que este caso hace al denominador de su formula ($n + 1$) igual a 0. A pesar de todos sus esfuerzos, Fermat nunca pudo llegar a resolver este caso.
La luz recién llegaría en el año 1661, cuando Christiaan Huygens se diera cuenta de que para el caso de $n = -1$, todos los rectángulos utilizados en la aproximación del área bajo la hipérbola, tenían la misma área, es decir que a medida que la distancia crece geométricamente desde 0, las área se incrementan en la misma proporción. Lo que implica que la relación entre el área y la distancia, es logarítmica!. Por tanto para resolver el problema del área de la hipérbola, $y = \frac{1}{x}$, simplemente deberíamos aplicar la función logarítmica sobre $x$; el único problema restante, era encontrar la base de esa función logarítmica, que como ya se pueden ir imaginando, no es ni nada más ni nada menos que el número $e$.
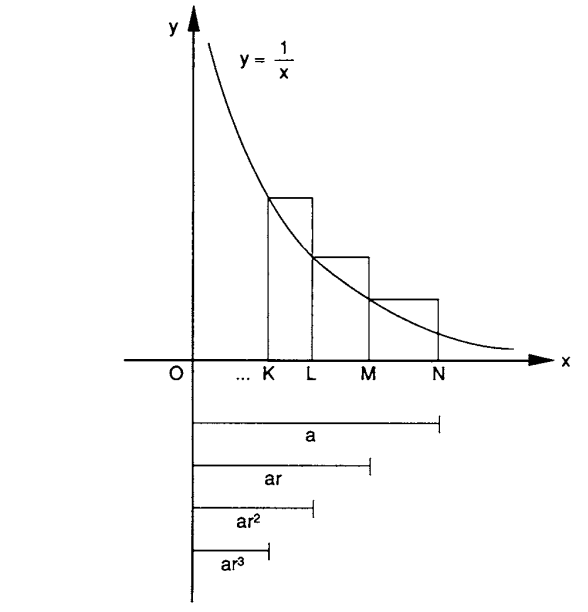
Es decir, que entonces para resolver el área bajo la hipérbola, debemos calcular el Logaritmo natural de $x$. Lo que llevado a la notación actual del cálculo integral equivale a decir que:
$$\int \left(\frac{1}{x}\right) \ dx = \ln (x)$$Desde este momento en adelante, $e$ comenzaría a convertirse en el amo y señor de los Logaritmos. Pero no se iba a quedar solo con eso, ya que aún quedaban por descubrirse otras importantes propiedades de este misterioso número.
Euler¶
Sin dudas, uno de los más grandes matemáticos de todos los tiempos fue Leonhard Euler. Prácticamente no dejó una rama de las Matemáticas sin tocar, dejando su marca en campos tan diversos como el análisis matemático, la teoría de números, la mecánica y la hidrodinámica, la cartografía, la topología, la óptica y la astronomía. A él también le debemos muchos de los símbolos matemáticos que usamos hoy en día, como ser, $i, \ f(x), \ \pi$ y el mismo símbolo del número $e$. La más influyente de sus numerosas obras fue su Introductio in analysin infinitorum, una obra en dos volúmenes publicados en 1748 y considerada como la base de análisis matemático moderno. En esta obra, Euler convierte a la función en el concepto central del análisis. Su definición de función es la que se suele utilizar hoy en día tanto en Matemáticas aplicadas, como en Física.
En el Introductio, Euler, hace notar por primera vez, el rol central que tiene el número $e$, y más precisamente la función exponencial $e^x$, y su función inversa, la función logarítmica $\ln x$ para el Cálculo. Euler puso a éstas dos últimas funciones en iguales condiciones, al darles definiciones independientes a cada una de ellas. Como ser:
$$e^x = \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n \\ \\ \\ \ln x = \lim_{n \to \infty} n(x^{1/n} - 1)$$Finalmente, a Euler también le debemos una de las ecuaciones más famosas e increíbles de todas las Matemáticas. La ecuación:
$$e^{i\pi} + 1 = 0$$En una sola fórmula, Euler logró conectar a las cinco más importantes constantes de las Matemáticas, y también tres de las más importantes operaciones matemáticas (adición, multiplicación y exponenciación). Las cinco constantes simbolizan las cuatro principales ramas de las Matemáticas clásicas: la Aritmética, representada por el 0 y el 1; el Álgebra por $i$; la Geometría, por $\pi$; y el Análisis, representado por $e$.
A partir de la obra de Euler, el número $e$, se convirtió también en amo y señor del Cálculo; gobernando así, tanto a los Logaritmos como al Análisis.
Calculando a $e$¶
Existen muchas maneras de calcular al número $e$, por ejemplo una forma de calcularlo es aplicando el siguiente límite:
$$e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n$$A medida que $n$ se va haciendo cada vez más grande, vamos ganando precisión en el cálculo de los decimales de $e$.
Como podemos ver, tanto del ejemplo numérico como del gráfico, esta definición de $e$, tarda bastante en converger hacia el valor exacto. Necesitamos un valor bastante grande de $n$ para ganar precisión.
Otra definición de $e$ que podemos utilizar para calcularlo y que converge mucho más rápido, es su definición como una serie infinita de factoriales.
$$e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!}+ \frac{1}{3!}+ \frac{1}{4!}+ \frac{1}{5!}+ \frac{1}{6!}+ \frac{1}{7!} + \dots$$Por último, también podríamos expresar a $e$, utilizando fracciones continuas, del siguiente modo:
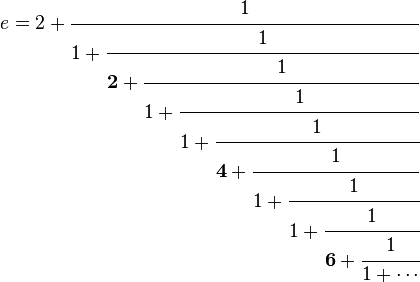
Al igual que ocurre con el número $\pi$ se conocen millones de dígitos del número $e$. Por ejemplo, para generar la imagen de la cabecera del artículo, yo utilicé 390 decimales de $e$.
$e$ en las finanzas¶
Como comenté a lo largo de todo el artículo, nos podemos topar con el número $e$ en infinidad de situaciones; pero una de las áreas donde más lo podemos encontrar es en la finanzas, ya que $e$ se encuentra escondido en la definición de una de las formulas más fundamentales del Cálculo financiero, la fórmula del interés compuesto. Por ejemplo, si repasamos la formula del valor futuro:
$$FV = PV \left(1 + \frac{r}{n}\right)^n$$donde $FV$ es el valor futuro; $PV$ es el valor presente de nuestra inversión; $r$ es la tasa de interés anual, expresada como valor decimal; y $n$ es el número de períodos.
Y si miramos detenidamente a esta ecuación, podemos ver cierta similitud con la definición de $e$ que dimos más arriba.
$$e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n$$Es más, si tomáramos el caso hipotético en el que el valor presente sea igual a 1, es decir $PV = 1$ y la tasa de interés sea del 100 %, $r = 1$. Podemos ver que la fórmula del valor futuro se convierte en la definición del número $e$!.
Por esta razón, al número $e$ lo vamos a encontrar en infinidad de situaciones en el Cálculo financiero. Por ejemplo, la definición de la fórmula de la capitalización continua utiliza al número $e$ explícitamente:
$$FV = PV \cdot e^{rt}$$donde $FV$ es el valor futuro; $PV$ es el valor presente de nuestra inversión; $r$ es la tasa de interés efectiva y $t$ es el tiempo de capitalización.
Éstos son sólo algunos casos, a medida que nos adentramos más en la complejidades del Cálculo financiero vamos a ver que $e$ continua apareciendo una y otra vez; pero eso va a quedar para próximos artículos!