Introducción¶
Cuando trabajamos en problemas de Machine Learning, muchas veces nos vamos a encontrar con enormes conjuntos de datos, con cientos o miles de características o features. Una forma simple de reducir las dimensiones de estas características es aplicar alguna técnica de Factorización de matrices. La Factorización de matrices tiene enormes aplicaciones en todo tipo de problemas relacionados a la inteligencia artificial, ya que la reducción de dimensionalidad es la esencia de la cognición.
Asimismo, la Factorización de matrices es también un tema unificador dentro del álgebra lineal numérica. Una amplia variedad de algoritmos se han desarrollado a lo largo de muchas décadas, proporcionando una plataforma numérica para operaciones de matrices tales como, la resolución de sistemas de ecuaciones lineales, la descomposición espectral, y la identificación de subespacios vectoriales. Algunos de estos algoritmos también han demostrado ser de utilidad en problemas de análisis estadístico de datos, como es el caso de la descomposición en valores singulares o SVD, por sus siglas en inglés, que es la base del análisis de componentes principales o PCA, que es una técnica muy utilizada para reducir el tamaño de los datos. Muchas investigaciones actuales en Machine Learning han centrados sus esfuerzos en el uso de la Factorización de matrices para mejorar el rendimiento de los sistemas de aprendizaje. Principalmente en el estudio de la factorización de matrices no negativas (NMF), la cual se centra en el análisis de matrices de datos cuyos elementos son positivos (no negativos), una ocurrencia muy común en los conjuntos de datos derivados de textos e imágenes.
¿Qué es la factorización de matrices?¶
En matemáticas, la factorización es una técnica que consiste en la descomposición de una expresión matemática (que puede ser un número, una matriz, un tensor, etc.) en forma de producto. Existen distintos métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que reciben el nombre de factores. Así por ejemplo, el número 6 se puede descomponer en el producto de 3 y 2. Si extendemos este concepto al mundo de las matrices, entonces podemos decir que la Factorización de matrices consiste en encontrar dos o más matrices de manera tal que cuando se multipliquen nos devuelvan la matriz original. Por ejemplo:
$$\left(\begin{matrix}3 & 4 & 5\\6 & 8 & 10 \end{matrix}\right) = \left(\begin{matrix}1\\2 \end{matrix}\right) \cdot \left(\begin{matrix}3 & 4 & 5 \end{matrix}\right) $$Los métodos de Factorización de matrices han ganado popularidad últimamente al haber sido aplicados con éxito en sistemas de recomendación para descubrir las características latentes que subyacen a las interacciones entre dos tipos de entidades, como por ejemplo usuarios y películas. El algoritmo que ganó el desafío de Netflix fue un sistema basado en métodos de Factorización de matrices.
Factorización de matrices en sistemas de ecuaciones lineales¶
Dos de las Factorización de matrices más utilizadas y que tal vez mucha gente las haya escuchado nombrar alguna vez son la factorización LU y la factorización QR; las cuales se utilizan a menudo para resolver sistemas de ecuaciones lineales.
Factorización LU¶
$$A = LU$$En álgebra lineal, la factorización o descomposición LU (del inglés Lower-Upper) es una forma de factorización de una matriz como el producto de una matriz triangular inferior y una superior. La factorización LU expresa el método de Gauss en forma matricial. Así por ejemplo, tenemos que $PA = LU$ donde $P$ es una matriz de permutación. Una condición suficiente para que exista la factorización es que la matriz $A$ sea una matriz no singular.
En Python podemos encontrar la descomposición LU con la ayuda de SciPy de la siguiente forma:
# Ejemplo factorización LU
A = np.array([[7, 3, -1, 2]
,[3, 8, 1, -4]
,[-1, 1, 4, -1]
,[2, -4, -1, 6]])
P, L, U = la.lu(A)
# Matriz A
A
# Matriz de permutación
P
# Matriz triangular inferior
L
# Matriz triangular superior
U
# A = LU
L @ U
Factorización QR¶
$$A = QR$$La descomposición o factorización QR consiste en la descomposición de una matriz como producto de una matriz ortogonal ($Q^T \cdot Q = I$) por una matriz triangular superior. la factorización QR es ampliamente utilizada en las finanzas cuantitativas como base para la solución del problema de los mínimos cuadrados lineales, que a su vez se utiliza para el análisis de regresión estadística.
En Python podemos encontrar la descomposición QR con la ayuda de SciPy de la siguiente forma:
# Ejemplo factorización QR
A = np.array([[12, -51, 4],
[6, 167, -68],
[-4, 24, -41]])
Q, R = la.qr(A)
# Matriz A
A
# Matriz ortogonal Q
Q
# Matriz triangular superior R
R
# A = QR
Q @ R
Matrices dispersas y no negativas¶
En muchas ocasiones cuando trabajamos con matrices para representar el mundo físico, nos vamos a encontrar con que muchas de estas matrices están dominadas por mayoría de elementos que son cero. Este tipo de matrices son llamadas matrices dispersas, es decir, matrices de gran tamaño en que la mayor parte de sus elementos son cero. Como sería ineficiente almacenar en la memoria de la computadora todos los elementos en cero, en las matrices dispersas solo vamos a almacenar los valores que no son cero y alguna información adicional acerca de su ubicación.
Asimismo muchos datos del mundo real son no negativos y los componentes ocultos correspondientes tienen un sentido físico solamente cuando son no negativos. En la práctica, ambas características, ser dispersas y no negativas son a menudo deseable o necesario cuando los componentes subyacentes tienen una interpretación física. Por ejemplo, en el procesamiento de imágenes y visión artificial, las variables involucradas y los parámetros pueden corresponder a píxeles, y la factorización de matrices dispersas y no negativas está relacionada con la extracción de las partes más relevantes de las imágenes. La representación dispersa de los datos por un número limitado de componentes es un problema importante en la investigación. En Machine Learning, las matrices dispersas está estrechamente relacionada con la selección de atributos y ciertas generalizaciones en algoritmos de aprendizaje; mientras que la no negatividad se relaciona a las distribuciones de probabilidad.
En Python, podemos representar a las matrices dispersas con la ayuda de scipy.sparse.
# Ejemplo matriz dispersa con scipy
A = sp.diags([1, -2, 1], [1, 0, -1], shape=[10, 10], format='csc')
A
A.data
A.indices
A.indptr
A.todense()
La descomposición en valores singulares (SVD) y el análisis de componentes principales (PCA)¶
El SVD y el PCA son herramientas ampliamente utilizadas, por ejemplo, en el análisis de imágenes médicas para la reducción de dimensionalidad, la construcción de modelos, y la comprensión y exploración de datos. Tienen aplicaciones en prácticamente todas las áreas de la ciencia, machine learning, procesamiento de imágenes, ingeniería, genética, computación cognitiva, química, meteorología, y redes neuronales, sólo por nombrar algunas; en dónde nos encontramos con grandes conjuntos de datos. El propósito del análisis de componentes principales PCA es derivar un número relativamente pequeño de combinaciones lineales no correlacionadas (componentes principales) de una conjunto de variables aleatorias de media cero mientras que conserva la mayor cantidad de información de las variables originales como sea posible. Entre los objetivos del PCA podemos encontrar los siguientes:
- Reducción de dimensionalidad.
- Determinación de combinaciones lineales de variables.
- Selección de características o features: la elección de las variables más útiles.
- Visualización de datos multidimensionales.
- Identificación de las variables subyacentes.
- Identificación grupos de objetos o de valores atípicos.
Veamos algunos ejemplos con Python
# Ejemplo SVD con scipy.linalg.svd
# Matriz A a factorizar
A = np.array([[2, 4]
,[1, 3]
,[0, 0]
,[0, 0]])
A
# Factorización con svd
# svd factoriza la matriz A en dos matrices unitarias U y Vh, y una
# matriz s de valores singulares (reales, no negativo) de tal manera que
# A == U * S * Vh, donde S es una matriz con s como principal diagonal y ceros
U, s, Vh = la.svd(A)
U.shape, Vh.shape, s.shape
# Matriz unitaria
U
# Valores singulares
s
# Matriz unitaria
Vh
# Generando S
S = la.diagsvd(s, 4, 2)
S
# Reconstruyendo la Matriz A.
U @ S @ Vh
# Ejemplo svd con iris dataset
iris = sns.load_dataset("iris")
print(iris.shape)
iris.head()
# Aplicando svd
U, s, Vh = sp.linalg.svds((iris - iris.mean()).iloc[:,:-1],2)
# Creando los componentes principales
pc = U @ np.diag(s)
pc = pc[:,::-1]
# graficando el dataset reducido a 2 componenetes
iris_svd = pd.concat((pd.DataFrame(pc, index=iris.index
, columns=('c0','c1')), iris.loc[:,'species']),1)
g = sns.lmplot('c0', 'c1', iris_svd, hue='species', fit_reg=False, size=8
,scatter_kws={'alpha':0.7,'s':60})
# Ejemplo de PCA con Scikit-Learn e Iris dataset
# Divido el dataset en datos y clases
X = iris.ix[:,0:4].values
y = iris.ix[:,4].values
# Estandarizo los datos
X_std = StandardScaler().fit_transform(X)
pca = PCA(n_components=2)
Y_pca = pca.fit_transform(X_std)
# Visualizo el resultado
for lab, col in zip(('setosa', 'versicolor', 'virginica'),
('blue', 'red', 'green')):
plt.scatter(Y_pca[y==lab, 0],
Y_pca[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Componente 1')
plt.ylabel('Componente 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.title('Ejemplo PCA')
plt.show()
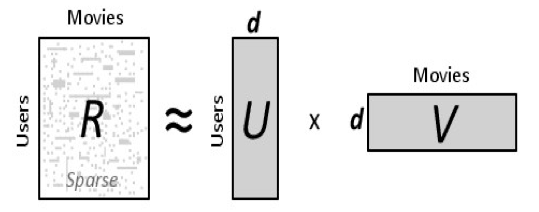
Factorización de matrices en sistemas de recomendación¶
En un sistemas de recomendación como Netflix o MovieLens, hay un grupo de usuarios y un conjunto de elementos (películas en los dos sistemas anteriores). Teniendo en cuenta que cada usuario ha valorado algunos elementos en el sistema, nos gustaría predecir cómo los usuarios calificarían los artículos que aún no se han valorado, de tal manera que podemos hacer recomendaciones a los usuarios. En este caso, toda la información que tenemos sobre las calificaciones existentes pueden ser representados en una matriz. Supongamos ahora que tenemos 5 usuarios y 4 películas y las calificaciones son números enteros de 1 a 5, la matriz resultante puede ser algo como la siguiente (el guión significa que el usuario aún no ha calificado la película):
| P1 | P2 | P3 | P4 | |
| U1 | 5 | 3 | - | 1 |
| U2 | 4 | - | - | 1 |
| U3 | 1 | 1 | - | 5 |
| U4 | 1 | - | - | 4 |
| U5 | - | 1 | 5 | 4 |
Por lo tanto, la tarea de predecir las calificaciones que faltan se puede considerar como un problema de llenar los espacios en blanco (los guiones en la matriz) de tal manera que los valores resultantes serían consistentes con las calificaciones existentes en la matriz.
La intuición detrás de usar Factorización de matrices para resolver este problema es que deberían existir algunas características latentes que determinen cómo un usuario califica una película. Por ejemplo, dos usuarios darían una alta calificación a una cierta película si a ambos les gusta los actores / actrices de la película, o si la película es una película de acción, que es un género preferido por ambos usuarios. Por lo tanto, si podemos descubrir estas características latentes, deberíamos ser capaces de predecir una calificación con respecto a un determinado usuario y una cierta película, porque las características asociadas con el usuario deben coincidir con las características asociadas con la película.
Al tratar de descubrir las diferentes características latentes, estamos suponiendo implícitamente que el número de características va a ser menor que el número de usuarios y el número de elementos. No debería ser difícil de entender este supuesto ya que no sería razonable que cada usuario está asociado con una característica única (aunque esto no es imposible). Y de todos modos, si este es el caso, no tendría sentido hacer recomendaciones, porque ninguno de estos usuarios estarían interesados en los artículos calificados por otros usuarios.
Si llevamos este ejemplo sencillo a Python, podríamos modelarlo utilizando Scikit-learn NMF o Nimfa.
# Ejemplo en python
# Matriz de ratings de los usuarios
R = np.array([[5, 3, 0, 1]
,[4, 0, 0, 1]
,[1, 1, 0, 5]
,[1, 0, 0, 4]
,[0, 1, 5, 4]])
# Armado del modelo
modelo = NMF(n_components= 2, init='random',random_state=1982,
alpha=0.0002, beta=0.02, max_iter=5000)
U = modelo.fit_transform(R)
V = modelo.components_
# Reconstrucción de la matriz
U @ V
# Error del modelo
modelo.reconstruction_err_
# Ejemplo utilizando nimfa
snmf = nimfa.Snmf(R, seed="random_vcol", rank=2, max_iter=30, version='r', eta=1.,
beta=1e-4, i_conv=10, w_min_change=0)
# Armando el modelo
fit = snmf()
U = fit.basis()
V = fit.coef()
# Reconstruyendo la matriz
np.around(U @ V, decimals=2)
Librerías de Python para factorización de matrices¶
Para concluir, podemos enumerar algunas de las librerías de Python que nos pueden ser de mucha utilidad a la hora de trabajar con Factorización de matrices, como ser:
- NumPy: El popular paquete matemático de Python, nos va a permitir crear vectores, matrices y tensores; y poder manipularlos y realizar operaciones sobre ellos con mucha facilidad.
- SciPy: El paquete que agrupa un gran número de herramientas científicas en Python. Nos va a permitir crear matrices dispersas y realizar factorizaciones con facilidad.
- Scikit-learn: Es una librería especializada en algoritmos para data mining y machine learning. Principalmente el submódulo de Descomposiciones en dónde vamos a encontrar las herramientas para reducciones de dimensionalidad.
- SymPy: Esta librería nos permite trabajar con matemática simbólica, convierte a Python en un sistema algebraico computacional. Nos va a permitir trabajar con las factorizaciones en forma analítica.
- Nimfa: Nimfa es una librería para factorización de matrices no negativas. Incluye las implementaciones de varios métodos de factorización, enfoques de inicialización y calificación de calidad. Soporta representaciones tanto de matrices densas como dispersas. Se distribuye bajo licencia BSD.
Con esto termina este artículo, espero les haya parecido interesante y les sea de utilidad en sus proyectos.
Saludos!
Este post fue escrito utilizando IPython notebook. Pueden descargar este notebook o ver su version estática en nbviewer.