El dia Pi

Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Mi blog sobre Python. El contenido esta bajo la licencia BSD.

Hoy, 14 de Marzo se celebra el día de Pi(\(\pi\)), esta celebración fue una ocurrencia del físico Larry Shaw, quien eligió esta fecha por su semejanza con el valor de dos dígitos de Pi. (en el formato de fecha de Estados Unidos, el 14 de Marzo se escribe 3/14). Particularmente este año, se dará el fenómeno de que será el día de Pi más preciso del siglo, ya que a las 9:26:53 se formaría el número Pi con 9 dígitos de precisión! (3/14/15 9:26:53). En honor a su día, voy a dedicar este artículo al número \(\pi\).

¿Qué es el número \(\pi\)?#

El número \(\pi\) es uno de los más famosos de la matemática. Mide la relación que existe entre la longitud de una circunferencia y su diámetro. No importa cual sea el tamaño de la circunferencia, esta relación siempre va a ser la misma y va a estar representada por \(\pi\). Este tipo de propiedades, que se mantienen sin cambios cuando otros atributos varían son llamadas constantes. \(\pi\) es una de las constantes utilizadas con mayor frecuencia en matemática, física e ingeniería.

Historia del número \(\pi\)#

La primera referencia que se conoce de \(\pi\) data aproximadamente del año 1650 ac en el Papiro de Ahmes, documento que contiene problemas matemáticos básicos, fracciones, cálculo de áreas, volúmenes, progresiones, repartos proporcionales, reglas de tres, ecuaciones lineales y trigonometría básica. El valor que se asigna a \(\pi\) en ese documento es el de 28/34 aproximadamente 3,1605.

Una de las primeras aproximaciones fue la realizada por Arquímedes en el año 250 adC quien calculo que el valor estaba comprendido entre 3 10/71 y 3 1/7 (3,1408 y 3,1452) y utilizo para sus estudios el valor 211875/67441 aproximadamente 3,14163.

El matemático Leonhard Euler adoptó el conocido símbolo \(\pi\) en 1737 en su obra Introducción al cálculo infinitesimal e instantáneamente se convirtió en una notación estándar hasta hoy en día.

¿Qué hace especial al número \(\pi\)?#

Lo que convierte a \(\pi\) en un número interesante, es que se trata de un número irracional, es decir, que el mismo no puede ser expresado como una fraccion de dos números enteros. Asimismo, también es un número trascendental, ya que no es raíz de ninguna ecuación algebraica con coeficientes enteros, lo que quiere decir que tampoco puede ser expresado algebraicamente.

Calculando el valor de \(\pi\)#

Si bien el número \(\pi\) puede ser observado con facilidad, su cálculo es uno de los problemas más difíciles de la matemática y ha mantenido a los matemáticos ocupados por años. Actualmente se conocen hasta 10 billones de decimales del número \(\pi\), es decir, 10.000.000.000.000.

La aproximación de Arquímedes#

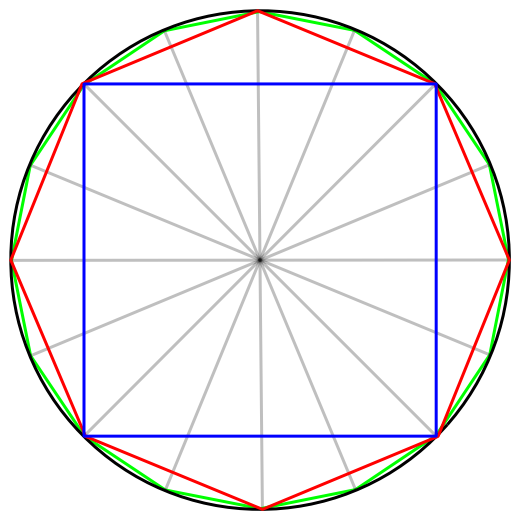
Uno de los métodos más conocidos para la aproximación del número \(\pi\) es la aproximación de Arquímedes; la cual consiste en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.

La serie de Leibniz#

Otro método bastante popular para el cálculo de \(\pi\), es la utilización de las series infinitas de Gregory-Leibniz. Este método consiste en ir realizando operaciones matematicas sobre series infinitas de números hasta que la serie converge en el número \(\pi\). Aunque no es muy eficiente, se acerca cada vez más al valor de Pi en cada repetición, produciendo con precisión hasta cinco mil decimales de Pi con 500000 repeticiones. Su formula es muy simple.

Calculando \(\pi\) con Python#

Como este blog lo tengo dedicado a Python, obviamente no podía concluir este artículo sin incluir distintas formas de calcular \(\pi\) utilizando Python; el cual bien es sabido que se adapta más que bien para las matemáticas!.

Como \(\pi\) es una constante con un gran número de sus dígitos ya conocidos, los principales módulos Matemáticos de Python ya incluyen su valor en una variable. Así por ejemplo, podemos ver el valor de \(\pi\) importando los módulos math o sympy.

# Pi utilizando el módulo math
import math
math.pi

3.141592653589793

# Pi utiizando sympy, dps nos permite variar el número de dígitos de Pi
from sympy.mpmath import mp
mp.dps = 33  # número de dígitos
print(mp.pi)

3.1415926535897932384626433832795

Si queremos calcular alguna aproximación al valor de \(\pi\), podríamos implementar por ejemplo la aproximación de Arquímedes de la siguiente manera.

# Implementacion de aproximación de Arquímedes
from decimal import Decimal, getcontext

def pi_archimedes(digitos):
    """
    Calcula pi utilizando el método de aproximacion de Arquímedes
    en n iteraciones.
    """
    def pi_archimedes_iter(n):
        """funcion auxiliar utilizada en cada iteracion"""
        polygon_edge_length_squared = Decimal(2)
        polygon_sides = 2
        for i in range(n):
            polygon_edge_length_squared = 2 - 2 * (1 - polygon_edge_length_squared / 4).sqrt()
            polygon_sides *= 2
        return polygon_sides * polygon_edge_length_squared.sqrt()
    
    #itera dependiendo de la cantidad de digitos
    old_result = None
    for n in range(10*digitos):
        # Calcular con doble precision
        getcontext().prec = 2*digitos
        result = pi_archimedes_iter(n)
        # Devolver resultados en precision simple.
        getcontext().prec = digitos
        result = +result # redondeo del resultado.
        if result == old_result:
            return result
        old_result = result

# Aproximacion de Arquímedes con 33 dígitos
print(pi_archimedes(33))

3.14159265358979323846264338327950

Por último, también podríamos implementar las series infinitas de Gregory-Leibniz, lo cual es realmente bastante sencillo.

def pi_leibniz(precision):
    """Calcula Pi utilizando las series infinitas de Gregory-Leibniz"""
    pi = 0
    modificador = 1
    for i in range(1, precision, 2):
        pi += ((4 / i) * modificador)
        modificador *= -1
    
    return pi

# Pi con una precision de 10000000 repeticiones.
print(pi_leibniz(10000000))

3.1415924535897797

Como se puede observar, el método de las series infinitas de Leibniz, si bien es de fácil implementación, no es muy preciso además de ser sumamente ineficiente.

Con esto concluyo y a festejar el día de \(\pi\)!!

Saludos!

Este post fue escrito utilizando IPython notebook. Pueden descargar este notebook o ver su version estática en nbviewer.