De tíos, primos, teoremas y conjeturas
Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Mi blog sobre Python. El contenido esta bajo la licencia BSD.
El tío Petros y la conjetura
Hace un tiempo atrás, quede atrapado en la lectura de la apasionante novela de Apostolos Doxiadis, El tío Petros y la conjetura de Goldbach. La novela trata basicamente de la relación entre un joven, en busca de su vocación, y su tío, quien en el pasado fue un prodigio de las matemáticas, pero que luego se recluyó de su familia y de la comunidad científica consumido por el intento solitario de demostrar uno de los problemas abiertos más difíciles de la teoría de números, la Conjetura de Goldbach. Lo que más me sorprendió del problema que consumió la vida del querido tío Petros, es lo simple que es su enunciado; la Conjetura de Goldbach nos dice que “Todo número par mayor que 2 puede escribirse como suma de dos números primos.”
Este enunciado, junto con la otra conjetura postulada por Goldbach, conocida como la Conjetura debil de Goldbach, que nos dice que “Todo número impar mayor que 5 puede expresarse como suma de tres números primos.”; trae a colación el concepto de los números primos como bloques constructores de los enteros.
Los números primos
Pero, ¿cómo es esto de que los números primos pueden ser considerados como bloques constructores de los números enteros?
Un número primo es un entero positivo que solo puede ser dividido en dos factores distintos, 1 y si mismo. De esta definición se desprende que el número 1 no es un número primo ya que solo puede ser dividido en un solo factor; en cambio, el número 2 si es primo, el único número primo que es par.
La idea de que los números primos pueden ser considerados como bloques constructores de los números enteros surge del enunciado del Teorema fundamental de la aritmética que nos dice que “Todo entero positivo puede ser representado de forma única como un producto de factores primos”; así por ejemplo el número \(28\) puede ser representado como \(2^2 * 7\); o el \(60\) como \(2^2 * 3 * 5\). Este teorema es un concepto fundamental en criptografía, los principales algoritmos de cifrado que se utilizan hoy en día residen en la factorización de primos, ya que es un proceso que requiere de mucho esfuerzo para calcularse mientras más grande sea el número que queremos factorizar.
Otro aspecto interesante de los números primos es que parecen surgir en forma aleatoria, hay veces que pueden aparecer en pares como (11, 13), (29, 31) o (59, 61) pero otras veces puede haber un largo intervalo entre ellos. Aún no se ha encontrado una formula que pueda predecir cual va a ser el próximo número primo. Como parece ser bastante difícil encontrar un patrón en los números primos, el esfuerzo de los matemáticos paso de intentar encontrar un patrón a intentar comprender la distribución de los números primos dentro de todos los enteros; es decir, intentar responder la pregunta de ¿Cuál es la probabilidad de que un número sea primo si elijo un número al azar en el rango de 0 a N?. Uno de los primeros en dar una respuesta bastante aproximada a esta pregunta fue Gauss, quien con tan solo 15 años de edad propuso la formula \(\pi(x)\approx\frac{x}{ln(x)}\) para responder a esa pregunta.
La formula propuesta Gauss implica que a medida que los números se hacen cada vez más grandes, los números primos son cada vez más escasos. Esto es lo que se conoce como teorema de los números primos. A pesar de que los números primos son cada vez más escasos mientras más grandes, siguen surgiendo indefinidamente, son infinitos; esto esta bien demostrado por el ya famoso teorema de Euclides; quien incluyo una de las más bellas demostraciones de las matemáticas en su obra Elementos en el 300 AC.
Encontrando los números primos
Para encontrar todos los números primos menores que un número N, uno de los algoritmos más eficientes y más fáciles de utilizar es lo que se conoce como la criba de Eratóstenes, el procedimiento que se utiliza consiste en crear una tabla con todos los números naturales comprendidos entre 2 y N, y luego ir tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. La siguiente animación describe el procedimiento graficamente.
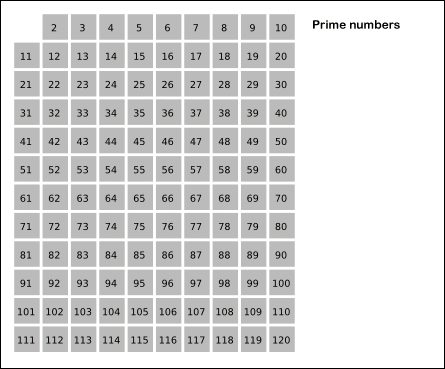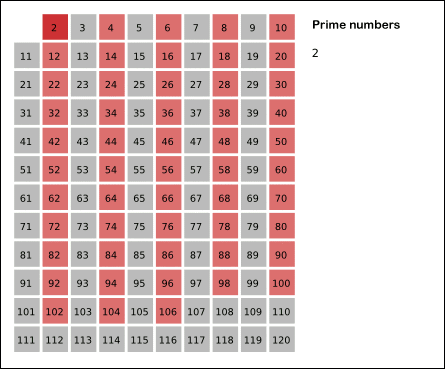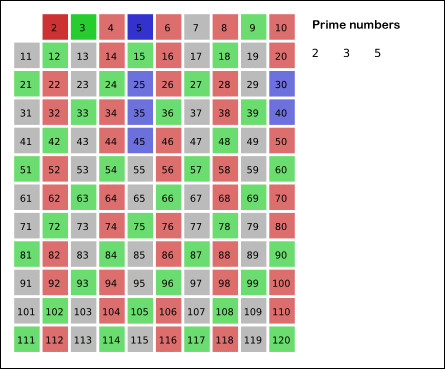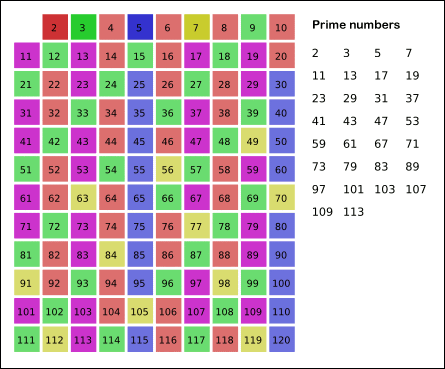
Ejemplo en Python
Veamos un ejemplo en Python de como implementar la criba de Eratóstenes y un proceso de factorización de primos.
# Factorizando primos en Python
import numpy as np
def criba_eratostenes(n):
"""Criba Eratostenes"""
l=[]
multiplos = set()
for i in range(2, n+1):
if i not in multiplos:
l.append(i)
multiplos.update(range(i*i, n+1, i))
return l
def factorizar_primos(n):
"""Factoriza un entero positivo en primos
>>>factorizar_primos(28)
[2, 2, 7]
"""
if n <=1:
return "Ingresar un entero mayor a 1"
factores = []
primos = criba_eratostenes(n)
pindex = 0
p = primos[pindex]
num = n
while p != num:
if num % p == 0:
factores.append(p)
num //= p
else:
pindex += 1
p = primos[pindex]
factores.append(p)
return factores
factorizar_primos(28) # Factores primos de 28
[2, 2, 7]
# Factores primos de 1982
factorizar_primos(1982)
[2, 991]
# Factores primos de 2015
factorizar_primos(2015)
[5, 13, 31]
La conjetura de Goldbach y Python
La Conjetura de Goldbach, es otro ejemplo de como también podemos construir todos los números enteros con simples operaciones aritméticas como la suma y no más que tres números primos. Al día de hoy, la conjetura continua sin poder ser demostrada; y es considerada uno de los problemas más difíciles de las matemáticas. La mayoría de los matemáticos estiman que es verdadera, ya que se ha mostrado cierta hasta por lo menos el \(10^{18}\); aunque algunos dudan que sea cierta para números extremadamente grandes, el gran Ramanujan dicen que se incluía en este último grupo.
Obviamente, como este blog esta dedicado a Python, no podría concluir este artículo sin incluir una implementación de la Conjetura de Goldbach en uno de los lenguajes que mejor se lleva con las matemáticas!
En esta implementación vamos a utilizar tres funciones, en primer lugar una criba de primos vectorizada utilizando numpy, para lograr un mejor rendimiento que con la criba de Eratóstenes del ejemplo anterior; y luego vamos a tener dos sencillas funciones adicionales, una que nos devuelva la composición de Goldbach para cualquier número par que le pasemos como parámetro.(esta función solo nos va a devolver la primer solución que encuentra, ya que pueden existir varias soluciones para algunos enteros pares). Por último, la restante función va a listar los resultados de la Conjetura de Goldbach para un rango de números enteros.
# La conjetura de Goldbach en Python
import numpy as np
def criba_primos(n):
"""Criba generadora de números primos.
Input n>=6, devuleve un array de primos, 2 <= p < n
"""
criba = np.ones(n / 3 + (n % 6 == 2), dtype=np.bool)
for i in range(1, int(n**0.5 / 3 + 1)):
if criba[i]:
k = 3 * i + 1 | 1
criba[k * k / 3::2 * k] = False
criba[k * (k - 2 * (i & 1) + 4) / 3::2 * k] = False
return np.r_[2, 3, ((3 * np.nonzero(criba)[0][1:] + 1) | 1)]
def goldbach(n):
"""imprime la composición de goldbach para n.
>>> goldbach(28)
(5, 23)
"""
primos = criba_primos(n)
lo = 0
hi = len(primos) - 1
while lo <= hi:
sum = primos[lo] + primos[hi]
if sum == n:
break
elif sum < n:
lo += 1
else:
hi -= 1
else:
print("No se encontro resultado de la conjetura de Goldbach para {}".format(n))
return primos[lo], primos[hi]
def goldbach_list(lower, upper):
"""Imprime la composición de Goldbach para todos los números pares
grandes que 'lower' y menores o iguales que 'upper'.
>>> goldbach_list(9,20)
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
"""
# La conjetura se aplica a pares mayores que 2.
if lower % 2 != 0:
lower += 1
if lower < 4:
lower = 4
if upper % 2 != 0:
upper -= 1
for n in range(lower, upper + 1, 2):
gb = goldbach(n)
print("{0} = {1} + {2}".format(n, gb[0], gb[1]))
# Goldbach entre 2000 y 2016
goldbach_list(2000, 2016)
2000 = 3 + 1997
2002 = 3 + 1999
2004 = 5 + 1999
2006 = 3 + 2003
2008 = 5 + 2003
2010 = 7 + 2003
2012 = 13 + 1999
2014 = 3 + 2011
2016 = 5 + 2011
# Goldbach entre 9.999.980 y 10.000.000
goldbach_list(9999980, 10000000)
9999980 = 7 + 9999973
9999982 = 11 + 9999971
9999984 = 11 + 9999973
9999986 = 13 + 9999973
9999988 = 17 + 9999971
9999990 = 17 + 9999973
9999992 = 19 + 9999973
9999994 = 3 + 9999991
9999996 = 5 + 9999991
9999998 = 7 + 9999991
10000000 = 29 + 9999971
# Goldbach entre 99.999.980 y 100.000.000
goldbach_list(99999980, 100000000)
99999980 = 193 + 99999787
99999982 = 11 + 99999971
99999984 = 13 + 99999971
99999986 = 139 + 99999847
99999988 = 17 + 99999971
99999990 = 19 + 99999971
99999992 = 3 + 99999989
99999994 = 5 + 99999989
99999996 = 7 + 99999989
99999998 = 67 + 99999931
100000000 = 11 + 99999989
Con esto termino, el que quiera puede divertirse intentando comprobar la Conjetura de Goldbach, aunque corre el riesgo de terminar desperdiciando su tiempo como el bueno del tío Petros en la novela. Espero que les haya parecido interesante el artículo.
Saludos!
Este post fue escrito utilizando IPython notebook. Pueden descargar este notebook o ver su versión estática en nbviewer.
