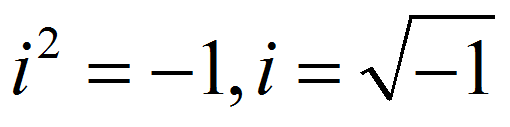
Introducción¶
Si bien el conjunto de los números reales $\mathbb{R}$, parece contener todos los números que podríamos llegar a necesitar. Existe todavía una dificultad, el hecho de que sólo se pueden tomar raíces cuadradas de los números positivos (o cero) y no de los negativos. Desde el punto de vista matemático resultaría conveniente poder extraer raíces cuadradas de números negativos tanto como de números positivos. Por tal motivo, que tal si "inventamos" una raíz cuadrada para el número -1 y la expresamos con el símbolo "$i$", de modo que tenemos
$$i^2 = -1$$La cantidad $i$ no puede ser, por supuesto, un número real puesto que el producto de un número real por sí mismo es siempre positivo (o cero, si el propio número es el cero). Por esta razón se ha aplicado convencionalmente el término "imaginario" a los números cuyos cuadrados son negativos. Sin embargo, es importante resaltar el hecho de que estos números imaginarios no son menos reales que los números reales a los que estamos acostumbrados.
Cuando estos números imaginarios se combinan con los números reales obtenemos lo que se conoce como números complejos; de esta forma, los números complejos vienen a completar a los números reales y nos permiten realizar todo tipo de operaciones algebraicas.
¿Qué es un número complejo?¶
Los números complejos incluyen todas las raíces de los polinomios, a diferencia de lo que pasaba cuando solo teníamos a los números reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario, el cual es un múltiplo real de la unidad imaginaria, que se indica con la letra $i$. O sea, que los números complejos tienen la forma
$$a + bi$$donde a y b son números reales llamados parte real y parte imaginaria , respectivamente, del número complejo. Las reglas para sumar y multiplicar tales números se siguen de las reglas ordinarias del álgebra, con la regla añadida de que $ i^2 = -1$. Veamos las distintas operaciones matemáticas que podemos hacer con estos números.
Operaciones con números complejos¶
Las operaciones que podemos realizar con los números complejos son las siguientes:
Suma¶
Para sumar dos números complejos simplemente sumamos cada elemento en forma separada. Es decir que:
$$(a+bi) + (c+di) = (a+c) + (b+d)i$$Así, por ejemplo $(2 + 2i) + (1 + 5i) = 3 + 7i$.
Producto por escalar¶
Para calcular el producto escalar de un número complejo, multiplicamos al escalar por cada una de sus partes, la real y la imaginaria. Es decir que:
$$r(a+bi) = (ra) + (rb)i$$Así, por ejemplo $ 3(2 + 3i) = 6 + 9i$.
Multiplicación¶
Para multiplicar dos números complejos, debemos realizar su multiplicación binomial. Es decir que:
$$(a+bi)(c+di) = ac + adi + bci + bdi^2$$En este punto, debemos recordad que $i^2$ es igual a -1; lo que nos facilita la solución del cálculo de la multiplicación. También existe una formula más simple para obtener el resultado de la multiplicación de dos números complejos, que es:
$$(a+bi)(c+di) = (ac-bd) + (ad+bc)i$$Así, por ejemplo $ (3 + 2i)(2 + 6i) = (3\times2 - 2\times6) + (3\times6 + 2\times2)i = -6 + 22i$.
Igualdad¶
Dos números complejos van a ser iguales si y solo si sus partes reales e imaginarias son iguales. Es decir que:
$$(a + bi) = (c + di) \iff a = c \wedge b = d$$Así, por ejemplo $ (3 + 2i) = (3 + 2i)$, ya que 3 = 3 y 2 = 2.
Resta¶
La resta de dos números complejos, funciona de forma similar a la suma.
$$(a+bi) - (c+di) = (a-c) + (b-d)i$$Así, por ejemplo $(2 + 2i) - (1 + 5i) = 1 -3i$.
Conjugado¶
El conjugado de un número complejo se obtiene cambiando el signo de su componente imaginario. Por lo tanto, el conjugado de un número complejo
$z = a + bi$, es $\overline{z} = a - bi$.
Para expresar que estamos buscando el conjugado, escribimos una línea sobre el número complejo. Así, por ejemplo
$$ \overline{ 2 + 3i} = 2 - 3i$$División¶
Para dividir dos números complejos, debemos utilizar el conjugado; ya que para realizar la división debemos multiplicar tanto el divisor como el dividendo por el conjugado del divisor. Así, por ejemplo si quisiéramos dividir:
$$\frac{2 + 3i}{4 - 5i}$$Debemos realizar el siguiente cálculo:
$$\frac{2 + 3i}{4 - 5i}\times\frac{4 + 5i}{4 + 5i}$$y teniendo en cuenta que la multiplicación de un número complejo por su conjugado, responde a la formula:
$$(a + bi)(a - bi) = a^2 + b^2$$Podemos resolver la división de la siguiente forma:
$$\frac{2 + 3i}{4 - 5i}\times\frac{4 + 5i}{4 + 5i} = \frac{8 + 10i + 12i + 15i^2}{16 + 25} = \frac{-7 + 22i}{41}$$Lo que nos lleva al resultado final:
$$ = \frac{-7}{41} + \frac{22}{41}i$$Para simplificar el procedimiento, y no tener que realizar tantos cálculos, podríamos utilizar la siguiente formula:
$$\frac{(a + bi)}{(c + di)} = {(ac+bd) + (bc-ad)i \over c^2+d^2} = \left({ac + bd \over c^2 + d^2} + {(bc - ad)i \over c^2 + d^2}\right)$$Valor absoluto o módulo de un número complejo¶
El valor absoluto, módulo o magnitud de un número complejo viene dado por la siguiente expresión:
$$ |a + bi| = \sqrt{a^2 + b^2} $$Así, por ejemplo $|4 + 3i| = \sqrt{16 + 9} = 5$.
Plano de los números complejos o Diagrama de Argand¶
El plano de Argand es un plano euclídeo ordinario con coordenadas cartesianas estándar $x$ e $y$ , donde $x$ indica la distancia horizontal (positiva hacia la derecha y negativa hacia la izquierda) y donde $y$ indica la distancia vertical (positiva hacia arriba y negativa hacia abajo). El número complejo $z = x + yi$ viene representado entonces por el punto del plano de Argand cuyas coordenadas son $( x , y )$.
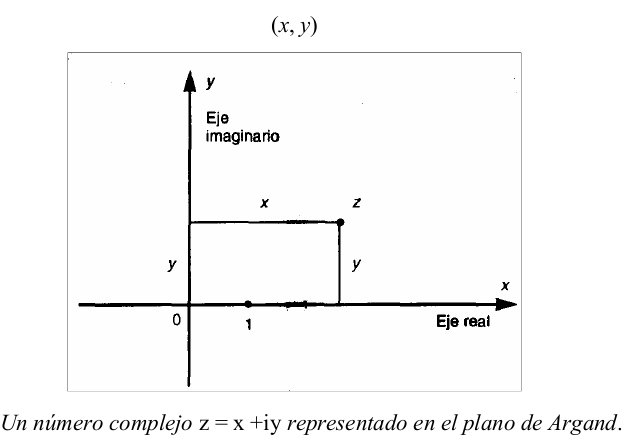
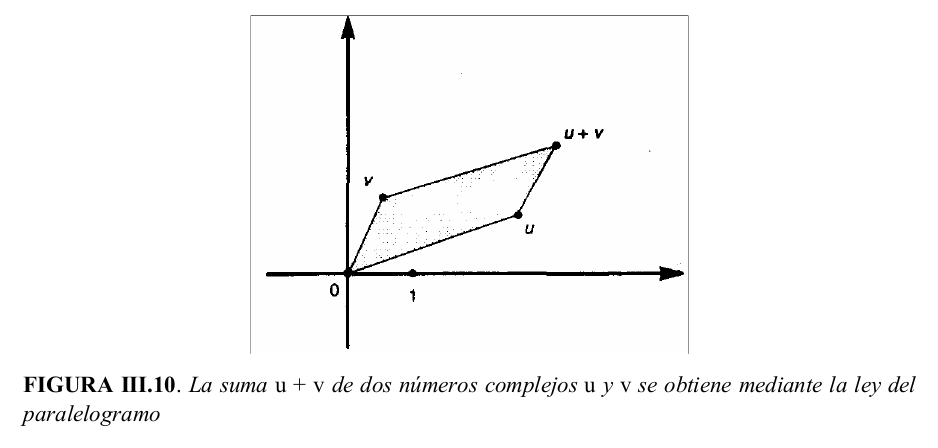
Nótese que 0 (considerado como un número complejo) viene representado por el origen de coordenadas, y 1 viene representado por un punto en el eje x. El plano de Argand proporciona simplemente un modo de organizar nuestra familia de números complejos en una imagen geométricamente útil. Las operaciones algebraicas básicas de la suma y multiplicación de números complejos encuentran ahora una forma geométrica clara. Consideremos por ejemplo la suma. Supongamos que $u$ y $v$ son dos números complejos representados en el plano de Argand de acuerdo con el esquema anterior. Entonces su suma $u + v$ viene representada como la suma vectorial de los dos puntos; es decir, el punto $u + v$ está en el lugar que completa el paralelogramo formado por $u, v$ y el origen 0.
Números complejos en Python¶
Python trae soporte por defecto para los números complejos, dónde la parte imaginaria va a estar representada por la letra j en lugar de utilizar la i como en la notación matemática. Veamos algunos ejemplos de las cosas que podemos hacer con ellos.
# Creando un número complejo
c1 = 4 + 3j
c1
# Verificando el tipo de dato
type(c1)
# Creando un número complejo con complex
c2 = complex(2, -3)
c2
# sumando dos números complejos
c1 = 2 + 2j
c2 = 1 + 5j
c1 + c2
# Restando dos números complejos
c1 - c2
# Producto escalar
c1 = 2 + 3j
3 * c1
# Multiplicando dos números complejos
c1 = 3 + 2j
c2 = 2 + 6j
c1 * c2
# Igualdad ente números complejos
c2 = 3 + 2j
c1 == c2
# Conjugado de un número complejo
c1 = 2 + 3j
c1.conjugate()
# División de números complejos
c1 = 1 + 1j
c2 = -1 + 1j
c1 / c2
# Valor absoluto o magnitud
c1 = 4 + 3j
abs(c1)
# Parte real
c1.real
# Parte imaginaria
c1.imag
# Grafico en plano de argand
# Graficos embebidos
%matplotlib inline
import matplotlib.pyplot as plt
def move_spines():
"""Crea la figura de pyplot y los ejes. Mueve las lineas de la izquierda y de abajo
para que se intersecten con el origen. Elimina las lineas de la derecha y la de arriba.
Devuelve los ejes."""
fix, ax = plt.subplots()
for spine in ["left", "bottom"]:
ax.spines[spine].set_position("zero")
for spine in ["right", "top"]:
ax.spines[spine].set_color("none")
return ax
ax = move_spines()
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.grid()
ax.scatter(c1.real, c1.imag)
plt.title("Plano de Argand")
plt.show()
Aplicaciones de los números complejos¶
Dado que los números complejos proporcionan un sistema para encontrar las raíces de polinomios y los polinomios se utilizan como modelos teóricos en diversos campos, los números complejos gozan de un gran importancia en varias áreas especializadas. Entre estas áreas especializadas se encuentran la ingeniería, la ingeniería eléctrica y la mecánica cuántica. Algunos temas en los que se utilizan números complejos incluyen la investigación de la corriente eléctrica, longitud de onda, el flujo de líquido en relación a los obstáculos, el análisis de la tensión en las vigas, el movimiento de los amortiguadores en automóviles, el estudio de resonancia de las estructuras, el diseño de dinamos y motores eléctricos, y la manipulación de grandes matrices utilizadas en el modelado. Por ejemplo, en ingeniería electrica para el análisis de circuitos de corriente alterna, es necesario representar cantidades multidimensionales. Con el fin de realizar esta tarea, los números escalares fueron abandonados y los números complejos se utilizan para expresar las dos dimensiones de frecuencia y desplazamiento de fase.
Así, por ejemplo si sabemos que el voltaje en un circuito es 45 + 10j voltios y la impedancia es de 3 + 4j ohms. Si queremos saber cual es la corriente, simplemente deberíamos resolver la ecuación $E = I \dot Z$ donde E es la tensión, I es la corriente, y Z es la impedancia. Reemplazando los términos en la formula, obtenemos que:
$$ I = \frac{45 + 10j}{3 + 4j}$$# Calculando I
I = (45 + 10j) / (3 + 4j)
I
Por tanto, la corriente es de 7 - 6j amps.
Además de todas estas aplicaciones, los números complejos nos permiten también realizar uno de los gráficos más hermosos de las matemáticas como es el fractal de Julia!!.
# importando librerías necesarias
import numpy as np
import numba
# Graficando el fractal de Julia
def py_julia_fractal(z_re, z_im, j):
'''Crea el grafico del fractal de Julia.'''
for m in range(len(z_re)):
for n in range(len(z_im)):
z = z_re[m] + 1j * z_im[n]
for t in range(256):
z = z ** 2 - 0.05 + 0.68j
if np.abs(z) > 2.0:
j[m, n] = t
break
jit_julia_fractal = numba.jit(nopython=True)(py_julia_fractal)
N = 1024
j = np.zeros((N, N), np.int64)
z_real = np.linspace(-1.5, 1.5, N)
z_imag = np.linspace(-1.5, 1.5, N)
jit_julia_fractal(z_real, z_imag, j)
fig, ax = plt.subplots(figsize=(8, 8))
ax.imshow(j, cmap=plt.cm.RdBu_r, extent=[-1.5, 1.5, -1.5, 1.5])
ax.set_xlabel("$\mathrm{Re}(z)$", fontsize=18)
ax.set_ylabel("$\mathrm{Im}(z)$", fontsize=18)
plt.show()
O el también famoso conjunto de Mandelbrot.
# Graficando el conjunto de Mandelbrot
def mandelbrot( h,w, maxit=20 ):
'''Crea el grafico del fractal de Mandelbrot del tamaño (h,w).'''
y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
c = x+y*1j
z = c
divtime = maxit + np.zeros(z.shape, dtype=int)
for i in range(maxit):
z = z**2 + c
diverge = z*np.conj(z) > 2**2
div_now = diverge & (divtime==maxit)
divtime[div_now] = i
z[diverge] = 2
return divtime
plt.figure(figsize=(8,8))
plt.imshow(mandelbrot(2000,2000))
plt.show()