Hasta el infinito y más alla
Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Matemáticas, análisis de datos y python. El contenido esta bajo la licencia BSD.

La línea consta de un número infinito de puntos; el plano, de un número infinito de líneas; el volumen, de un número infinito de planos; el hipervolumen, de un número infinito de volúmenes… No, decididamente no es éste… el mejor modo de iniciar mi relato.
Jorge Luis Borges - El libro de arena
Introducción
El concepto de infinito ha obsesionado a la mente humana por miles de años. La idea de que las cosas pueden seguir y seguir para siempre, que pueden no tener ni principio ni final, ni centro, ni límites; desafía a la intuición. Científicos, filósofos y teólogos por igual, han tratado de entenderlo, de cortar su tamaño, de averiguar su forma y dimensión; y en última instancia, de decidir si es un concepto bienvenido en nuestras descripciones del Universo que nos rodea. A pesar de todas las dificultades que puede traer el lidiar con el infinito, éste sigue siendo un tema fascinante. Se encuentra en el corazón de todo tipo de preguntas fundamentales del hombre. ¿Se puede vivir para siempre? ¿El universo tiene un final? ¿Tuvo un comienzo? ¿Tiene el universo un “borde” o simplemente no existen límites a su tamaño? Aunque es fácil pensar en las listas de números o secuencias de ’tics’ de un reloj que continúan para siempre, hay otros tipos de infinito que parecen ser más difíciles de concebir.
¿Qué es el infinito?
Generalmente existe la tendencia de pensar en el infinito simplemente como un número muy grande, sólo un poco más grande que el mayor número que se pueda imaginar, siempre fuera de su alcance; pero el infinito no es un número; sino que es un concepto, la idea de algo que no tiene fin.
El infinito en la matemáticas
Si bien el concepto de infinito parece ser un tema elusivo y complejo, aun así no a escapado a su estudio por parte de las matemáticas. Su estudio ya comenzó en la antigua Grecia, quienes con teoremas tales como que la cantidad de números primos no tiene límites, se enfrentaron ante la perspectiva de lo infinito. Aristóteles evitó la actualidad del infinito mediante la definición de una infinidad potencial, de forma de permitir que éstos teoremas continúen como válidos. Según esta distinción hecha por Aristóteles entre el infinito actual y el infito potencial, los números enteros son potencialmente infinitos porque siempre puede sumarse uno para conseguir un número mayor, pero el conjunto infinito de números enteros como tal, es decir el infinito actual de números enteros, no existe. Según los griegos el infinito actual nunca puede existir, sino que solo puede existir el infinito potencial; como reflejo del pensamiento griego, Aristóteles concluye que el infinito es imperfecto, inacabado e impensable. Esta definición de un infinito potencial y no real, funcionó y satisfizo a los matemáticos y filósofos por casi dos milenios.
Notación del infinito
El símbolo \(\infty\) que representa al infinito se lo debemos al matemático ingles John Wallis, quien fue un precursor del cálculo infinitesimal e introdujo la notación \(\infty\), que representa una curva sin fin, en el siglo diecisiete.
En camino hacia un mejor entendimiento del infinito
A medida que se continuaba explorando el concepto del infinito, nuevas paradojas continuaban apareciendo. En la edad media se entendía que un círculo más grande debería contener más puntos que un círculo más pequeño, sin embargo se puede encontrar una correspondencia de uno a uno entre los puntos de ambos círculos, como lo demuestra la siguiente figura:
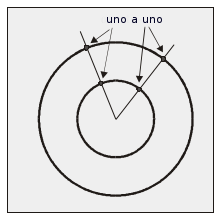
En 1600, Galileo entendió que el problema era el estar utilizando un razonamiento finito sobre cosas infinitas. Postuló que “Es un error hablar de cantidades infinitas como siendo la mayor o menor o igual que a la otra” y afirmó que el infinito no es un noción inconsistente, sino que obedece a reglas diferentes.
Otro de los temas que confundían a los matemáticos, era el comportamiento de las series infinitas, sobre todo aquellas que no eran convergentes. Recordemos que una serie es convergente cuando la suma de sus términos da como resultado un número finito; en caso contrario, se dice que la serie es divergente. Así por ejemplo la serie geométrica, sabemos que converge en 1, y se puede demostrar geométricamente:
$$\sum\limits_{i=1}^\infty\frac{1}{2^n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots = 1$$
Pero en cambio el resultado de la siguiente serie no se puede determinar:
$$ S = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 \dots $$Si por ejemplo agrupamos los términos de la siguiente forma, el resultado parece ser obviamente cero.
$$ S = (1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) \dots $$Pero si los agrupamos de esta otra forma, el resultado parece ser ahora claramente uno.
$$ S = 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) \dots $$y no termina acá, ya que incluso podríamos agrupar la serie del siguiente modo y el resultado sería \(\frac{1}{2}\).
$$\begin{eqnarray} S = 1 - ( 1 - 1 + 1 - 1 + 1 - 1 + 1 - \dots) \Rightarrow \\ S = 1 - S \Rightarrow 2S = 1 \Rightarrow S = \frac{1}{2} \end{eqnarray} $$es decir que el valor de la serie S, podría ser tanto 1, como 0, como \(\frac{1}{2}\).No es sorprendente que argumentos como éste, hacían que los matemáticos se pusieran muy nerviosos al tratar con los infinitos y quisieran evitarlos o incluso eliminarlos a toda costa.
Fuera de toda esta ambigüedad y confusión, la claridad surgió repentinamente en el siglo XIX, debido a los esfuerzos en solitario de un hombre brillante. Georg Cantor produjo una teoría que respondió a todas las objeciones de sus predecesores y reveló la riqueza inesperada escondida en el ámbito de lo infinito. De repente, los infinitos actuales se convirtieron en parte de las matemáticas.
Cantor y la teoría de conjuntos para explicar el infinito
Georg Cantor, aplicando ideas sumamente originales, postuló la teoría de conjuntos y utilizando el concepto de la cardinalidad de los conjuntos, se propuso explicar el concepto de infinito.
Segun la teoría de Cantor, dos conjuntos se dicen que tienen el mismo número de elementos, es decir, que tienen la misma cardinalidad, si existe una función definida entre ellos de forma tal que a cada elemento le corresponde sólo otro elemento del otro conjunto, y viceversa; o sea, que exista una correspondencia de uno a uno entre los elementos de ambos conjuntos. A partir de esta definición se puede establecer la idea de conjunto infinito. Se dice que un conjunto es infinito si existe un subconjunto con la misma cardinalidad que él. Esta definición plantea una contradicción con la intuición, pues todo subconjunto como parte del conjunto total parece que deba tener menos elementos. Eso es así, efectivamente, en los conjuntos finitos, pero no en los infinitos.
¿Distintos tipos de infinitos? Infinitos numerables y no numerables
Otro de los grandes aportes de Cantor, fue la distinción entre los infinitos numerables y no numerables. Cantor definió a los infinitos numerables como aquellos en los que se puede encontrar una correspondencia uno-a-uno con la lista de números naturales 1, 2, 3, 4, 5, 6,. . . Así, por ejemplo, los números pares son un infinito numerable, también lo son todos los números impares y ambos tienen el mismo tamaño. Por ejemplo, la correspondencia entre los primeros números impares sería la siguiente:
$$ \begin{eqnarray} 1 \longrightarrow 3 \\ 2 \longrightarrow 5 \\ 3 \longrightarrow 7 \\ 4 \longrightarrow 9 \\ 5 \longrightarrow 11 \\ 6 \longrightarrow 13 \\ 7 \longrightarrow 15 \\ 8 \longrightarrow 17 \\ 9 \longrightarrow 19 \\ 10 \longrightarrow \dots \\ \end{eqnarray} $$Por lo tanto, todos los conjuntos infinitos numerables tienen el mismo “tamaño” o cardinalidad en el sentido de Cantor. El también pensaba que éstos eran los infinitos más pequeños que pudieran existir y por lo tanto los representó utilizando la primera letra del alfabeto hebreo, el símbolo Aleph-cero, \(\aleph_{0}\). Un punto importante a tener en cuenta, es que esta definición excluye cualquier conjunto finito de objetos, ya que un conjunto finito sólo puede ponerse en correspondencia uno-a-uno con otro conjunto que contenga el mismo número de miembros. Este análisis llevó a algunas conclusiones sorprendentes. Cantor mostró que los números racionales, los cuales se forman al dividir un número entero por otro (por ejemplo \(\frac{1}{2}\), o \(\frac{13}{2}\)) son también un conjunto infinito numerable. El truco fue encontrar un sistema para poder contarlos sin perderse ninguno. Él utilizó el famoso proceso ahora conocido como la diagonal de Cantor para hacer esto. Fue contando cada uno de ellos de acuerdo al siguiente ordenamiento:

Cantor también pudo demostrar con un nuevo tipo de argumento matemático que existen infinitos más grandes y que no se pueden contar. Esto son los que hoy en día se conocen como infinitos no numerables. Dentro de esta categoría podemos encontrar al conjunto de los números reales, los cuales incluyen a los números irracionales, quienes no se pueden escribir como fracciones y tienen una expansión infinita de sus parte decimal.
Para demostrar que los números reales son un infinito no numerable, Cantor comenzó por suponer que se podían contar, lo que significaba que debería ser capaz de elaborar una receta sistemática para contar todos los decimales interminables que no terminaran en una cadena infinita de ceros. Los primeros de estos números podrían parecerse a éstos:
$$\begin{eqnarray} 1 \longrightarrow 0.\underline{2}34567891\dots \\ 2 \longrightarrow 0.5\underline{7}5603737\dots \\ 3 \longrightarrow 0.46\underline{3}214516\dots \\ 4 \longrightarrow 0.846\underline{2}16388\dots \\ 5 \longrightarrow 0.5621\underline{9}4632\dots \\ 6 \longrightarrow 0.46673\underline{2}271\dots \\ \dots \end{eqnarray} $$Luego creó un nuevo decimal tomando el primer dígito después del punto decimal del primer número, el segundo dígito del segundo número, y así sucesivamente para siempre(como por ejemplo los dígitos subrayados en la serie de arriba). Siguiendo el ejemplo, el nuevo decimal comenzaría como sigue:
\(0.273292\dots\)
Por último a este decimal recién creado, le sumó 1 a cada uno de sus infinitos dígitos. Obteniendo el número
\(0.384303\dots\)
El problema es que este número que acabó creando no puede aparecer en la lista ordenada original de todos los decimales que había asumido debía existir. Deberá ser distinto a cada número de la lista por lo menos en uno de sus dígitos, ya que fue construido expresamente de ese modo. Por lo tanto, los números reales (a veces llamados los números decimales o el continuo de números) no se pueden contar y son un infinito no numerable. Así mismo, también deben ser más grande que los números naturales o los números racionales. Cantor representó a este nuevo tipo de infinito con el símbolo \(\aleph_{1}\); ya que creía que no debía existir otro tipo de infinito que fuera mayor que el de los números naturales y menor que el de los números reales, aunque nunca fue capaz de demostrarlo. Esta es lo que se conoce como la hipótisis del continuo.
Este descubrimiento de Cantor, que existen infinitos de diferentes tamaños y se pueden distinguir de una manera completamente inequívoca, fue uno de los grandes descubrimientos de las matemáticas. También estaba completamente en contra de la opinión dominante de la época.
Una jerarquía de infinitos
Además de todos los grandes aportes que Cantor realizó a la comprensión del infinito, su descubrimiento más espectacular fue que los infinitos no sólo son incontables, sino que son insuperables!. Descubrió que debe existir una jerarquía ascendente interminable de infinitos. No hay uno más grande que todos que pueda contener a todos ellos. No hay un universo de universos que podemos anotar y capturar. Cantor fue capaz de demostrar que existe una jerarquía ascendente de infinitos sin fin, una jerarquía infinita de infinitos!. Para demostrar este punto, utilizó el concepto de conjunto potencia.
Recordemos que un conjunto potencia de un conjunto A, expresado por \(P_{A}\), es el conjunto formado por todos los distintos subconjuntos de A. Así por ejemplo el conjunto potencia del conjunto \(A={1,2,3}\); va a ser igual a \(P_{A}={\emptyset,{1},{2},{3},{1,2},{2,3}, {1,3},{1,2,3}}\). Un teorema importante de la teoría de conjuntos establece que si A es un conjunto con k elementos, es decir que n(A) = k; entonces el conjunto potencia de A tiene exactamente \(2^k\) elementos. En nuestro ejemplo anterior podemos ver que n(A)=3, por lo tanto \(n(P_{A}) = 2^3\), lo que es igual a los 8 elementos que vimos que tiene el conjunto potencia de A.
Entonces, si se toma cualquier conjunto infinito, siempre es posible generar una que es infinitamente más grande considerando a su conjunto potencia, es decir, el conjunto que contiene todos sus subconjuntos. Así, de un conjunto infinito como \(\aleph_{0}\) podemos crear un conjunto infinitamente más grande mediante la formación de su conjunto potencia, \(P_{\aleph_{0}}\). Luego podemos hacer lo mismo otra vez, formando el conjunto potencia de \(P_{\aleph_{0}}\), el cual será infinitamente más grande que \(P_{\aleph_{0}}\). Y así sucesivamente, sin fin. De esta forma las matemáticas crean una jerarquía sin fin de infinitos ascendentes . El infinito nunca puede ser capturado por las fórmulas. También muestra que el número de posibles verdades es infinito.
Hotel infinito
Una de las imágenes que se suele utilizar para ilustrar el concepto de infinito es el relato del hotel infinito ideado por el gran matemático David Hilber, el cual explica de manera simple e intuitiva, las paradojas relacionadas con el concepto del infinito.
El hotel infinito es un hotel como cualquier otro, con la única excepción de que cuenta con un número infinito de habitaciones!
Tan pronto se abrieron las puertas de este hotel la gente comenzó a abarrotarlo y pronto se encontraron con que el hotel de habitaciones infinitas se encontraba lleno de infinitos huéspedes. En ese momento surgió la primera paradoja, así que se tomó como medida que los huéspedes siempre tendrían habitación asegurada pero con el acuerdo previo de que tendrían que cambiar de habitación cada vez que se les pidiera. Fue entonces cuando llegó un nuevo huesped al hotel que ya se encontraba lleno. El hombre pidió su habitación y el recepcionista, consciente de que no habría ningún problema, tomó un micrófono por el que avisó a todos los huéspedes que por favor revisaran el número de su habitación, le sumaran uno y se cambiaran a ese número de habitación, de esta manera el nuevo huésped pudo dormir tranquilamente en la habitación número 1. Pero, ¿qué pasó entonces con el huésped que se encontraba en la última habitación? Sencillamente no hay última habitación ya que \(\infty + 1\) sigue siendo \(\infty\).
La segunda paradoja surgió cuando llegó un representante de una agencia de viajes solicitando hospedar a un infinito número de turistas en el hotel de infinitas habitaciones, las cuales ya estaban todas ellas ocupadas. Pero el recepcionista nuevamente no tuvo ningún problema, tomó el micrófono y pidió a todos los huéspedes que se mudaran a la habitación correspondiente al resultado de multiplicar por 2 el número de su habitación actual. De esa forma todos los huéspedes se mudaron a una habitación par, y todas las habitaciones impares quedaron libres. Como hay infinitos números impares, los infinitos turistas pudieron alojarse sin más problemas.
La tercer paradoja se presentó cuando llegó otro representante de la agencia de viajes aún más preocupado que el primero y avisó que ahora la agencia tenía un infinito número de excursiones con un infinito número de turistas cada una. ¿cómo podrían hospedar a un número infinito de infinitos turistas en un hotel que ya se encontraba lleno? El recepcionista permaneció inmutable, tomó tranquilamente el micrófono y se comunicó solamente con las habitaciones cuyo número fuera primo o alguna potencia de éstos (\(p^n\)), les pidió que elevaran el número 2 al número de la habitación en la que se encontraban (\(2^{p^n}\)) y se cambiaran a esa habitación. Entonces asignó a cada una de las excursiones un número primo (distinto de 2), a cada uno de los turistas de cada una de las excursiones un número impar (t), de manera que la habitación de cada uno de los turistas, se calculaba tomando el número primo de su excursión (p) y elevandolo al número que les tocó dentro de su excursión (t) lo que da \(p^t\). Existiendo un número infinito de números primos y un número infinito de números impares, fácilmente se logró hospedar a un número infinito de infinitos huéspedes dentro del hotel infinito.
Las paradojas de Zenón y el concepto de límite
Como venimos viendo, el concepto de infinito esta repleto de paradojas; y algunas de las más famosas de ellas son también de las más antiguas. Se las debemos a Zenón de Elea, quien fue discípulo del filósofo Parménides y por lo tanto sostenía, al igual que su maestro, que el universo era intemporal e inmutable y que por lo tanto el movimiento era solo una ilusión. Para sostener su tesis, Zenón de Elea propuso una serie de argumentos que hoy en día se conocen como las paradojas de Zenón.
La primera paradoja pretende demostrar que el movimiento es imposible, porque si quisiéramos caminar de un punto a otro, primero deberíamos cruzar la mitad de la distancia, luego la mitad de la distancia restante, luego la mitad del resto, y así sucesivamente. O sea, que si los dos puntos están a un kilómetro de distancia, en primer lugar debemos llegar a \(\frac{1}{2}\) km desde su inicio, a continuación, \(\frac{3}{4}\) km desde su inicio, luego a \(\frac{7}{8}\) km y así sucesivamente. Según el argumento de Zenón sólo se podría llegar si se toma un número infinito de pasos; y como los griegos rechazaban el infinito, por lo tanto deberíamos rechazar el movimiento también y concluir que este no es posible.
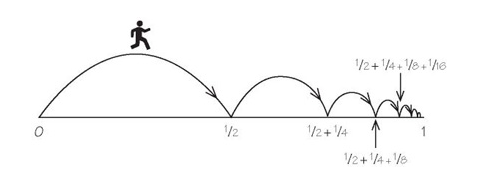
En su segunda paradoja, Zenón crea el escenario de una carrera entre el famoso atleta Aquiles y un rival mucho más lento, una tortuga. Aquiles comienza en la posición 0, mientras que la tortuga, que sólo puede correr a la mitad de la velocidad de Aquiles, tiene una ventaja inicial de un kilómetro. Ambos comienzan a correr al mismo tiempo. De acuerdo al planteamiento de este escenario, podríamos pensar que Aquiles, al correr el doble de rápido que la tortuga, la superaría en la marca de 2 kilómetros. Sin embargo, cuando Aquiles llega a la marca de 1 km, la tortuga ya ha avanzado a \(1 + \frac{1}{2}\) km; cuando Aquiles llega al punto \(1\frac{1}{2}\) km, la tortuga ha alcanzado \(1 + \frac{1}{2} + \frac{1}{4}\) km; y así sucesivamente. Cuando, después de N pasos, Aquiles alcanza una distancia de \(2 - \frac{1}{2}^{N-1}\) desde el punto inicial, la tortuga se encuentra todavía en la delantera, ya que está a una distancia de \(2 - \frac{1}{2}^{N+1}\). No importa lo grande que sea N (el número de divisiones del viaje), Aquiles nunca se adelanta a la tortuga!
Resolviendo las paradojas
Para poder resolver estas paradojas, debemos recurrir al cálculo infinitesimal, y más particularmente al concepto de límite. El límite de una sucesión es la noción intuitiva de que la sucesión se aproxima arbitrariamente a un único punto o valor. Es decir, que la sucesión va a converger en un valor determinado. En el caso de las dos paradojas de Zenón, nos encontramos ante series geométricas, las cuales ya vimos que tienen un límite y convergen en un valor finito. Por tanto se puede demostrar que Aquiles realmente alcanzará a la tortuga. Los tiempos en los que Aquiles recorre la distancia que lo separa del punto anterior en el que se encontraba la tortuga son cada vez más y más pequeños (hasta el infinito más pequeños), y su suma da un resultado finito, que es el momento en que alcanzará a la tortuga.
Límites al infinito
Como pudimos ver a lo largo de todo el artículo, el infinito es un concepto muy especial. Sabemos que no podemos llegar a el, pero todavía podemos tratar de averiguar el valor de las funciones o sucesiones que tratan con el infinito. Por ejemplo, si quisiéramos saber cual es el resultado de \(\frac{1}{\infty}\), deberíamos responder que no existe solución, ya que el infinito no es un número, y por lo tanto no podríamos determinar el resultado de esa operación. Sin embargo, a pesar de que no podemos trabajar con el infinito en sí mismo, podemos aproximarnos bastante a el y ver que sucede a medida que vamos dividiendo a uno por valores cada vez más grandes. Por ejemplo, si reemplazamos al \(\infty\), por \(x\), tendríamos una ecuación a la que podríamos ir aplicando valores cada vez más grandes de \(x\) y ver a que resultado llegamos. Ayudándonos de nuestro buen amigo Python podríamos ver los resultados fácilmente y comprobar que a medida que \(x\) se hace cada vez más grande, el valor de la función \(\frac{1}{x}\) se aproxima cada vez más a cero.
Ver Código
# <!-- collapse=True -->
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def f(x):
return x**-1.0 # 1/x == x**-1
x = np.array([1, 2, 4, 10, 100, 1000, 10000, 100000, 1000000 ])
y = f(x)
# Construyendo tabla de valores x e y con pandas
tabla = pd.DataFrame(x, columns=['x'])
tabla['1/x'] = y
tabla
| x | 1/x | |
|---|---|---|
| 0 | 1 | 1.000000 |
| 1 | 2 | 0.500000 |
| 2 | 4 | 0.250000 |
| 3 | 10 | 0.100000 |
| 4 | 100 | 0.010000 |
| 5 | 1000 | 0.001000 |
| 6 | 10000 | 0.000100 |
| 7 | 100000 | 0.000010 |
| 8 | 1000000 | 0.000001 |
# <!-- collapse=True -->
# Graficando 1/x
x = np.arange(1, 1000) # Rango de valores de x
plt.figure(figsize=(8,6))
plt.title(r"Graficando $\frac{1}{x}$")
plt.xlabel('x')
plt.ylabel(r"$f(x) = \frac{1}{x}$")
plt.plot(x, f(x), label=r"$\frac{1}{x}$ tiende a cero a medida que x crece")
plt.ylim([0, .12])
plt.legend()
plt.show()
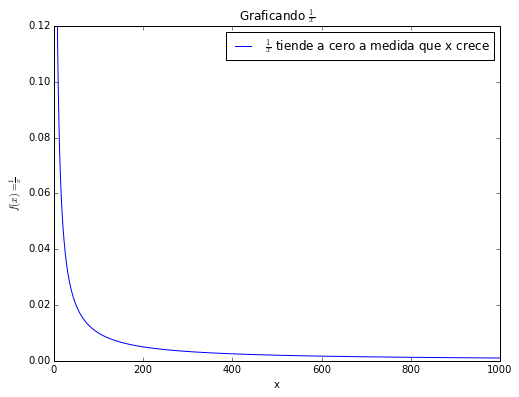
Como nos muestran tanto los cálculos como el gráfico, a medida que vamos aumentando el valor de \(x\), la función \(\frac{1}{x}\) se va aproximando cada vez más a cero. Por tanto podemos conjeturar que la función \(\frac{1}{x}\) tiende a cero. Si bien, no podemos decir que pasa en el infinito, si podemos decir que pasa a medida que nos vamos acercando cada vez más a él. Por tanto podríamos decir que a medida que el valor \(x\) tiende a \(\infty\), el valor de la función \(\frac{1}{x}\), se aproxima a su límite cero. En el lenguaje de las matemáticas, lo expresaríamos de la siguiente forma:
$$\lim_{x\to \infty} \left(\frac{1}{x}\right) = 0$$El concepto de Límite es una de las herramientas principales sobre las que se sustenta el cálculo. Muchas veces, una función puede ser indefinida en un punto, pero podemos pensar en lo que pasa a medida que la función “se acerca” cada vez más a ese punto. Otras veces, la función puede ser definida en un punto, pero puede aproximarse a un límite diferente.
Con esto termina este artículo, para concluir cerremos la curva sin fin que representa al infinito con otra frase de Borges, que fue con quien comenzamos el artículo!
Hay un concepto que es el corruptor y el desatinador de los otros. No hablo del Mal cuyo limitado imperio es la ética; hablo del infinito.
Jorge Luis Borges - Avatares de la tortuga
Espero les haya parecido interesante y no se hayan sentido tan desconcertados al toparse con el concepto de infinito como la probe serpiente pitón de la cabecera del artículo!.
Saludos!
Este post fue escrito utilizando IPython notebook. Pueden descargar este notebook o ver su version estática en nbviewer.