Introducción al Cálculo con Python

Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Matemáticas, análisis de datos y python. El contenido esta bajo la licencia BSD.

Cálculo con python

Introducción

El Cálculo es una rama muy importante de la Matemática moderna; tiene profundas raíces en problemas físicos y gran parte de su potencia y belleza derivan de la variedad de sus aplicaciones. Las subramas conocidas como Cálculo integral y Cálculo diferencial son instrumentos naturales y poderosos para atacar múltiples problemas que surgen en Física, Astronomía, Ingeniería, Química, Geología, Biología, y en otros campos de las ciencias. El Cálculo no sólo es un instrumento técnico, sino que contiene una colección de ideas fascinantes y atrayentes que han ocupado el pensamiento humano durante cientos de años. Estas ideas están relacionadas con la velocidad, el área, el volumen, la razón de crecimiento, la tangente a una línea, y demás.

Historia

El origen del Cálculo se remonta a más de 2300 años, cuando los griegos intentaban resolver el problema del área ideando el procedimiento que llamaron método de exhaución. La idea esencial de este método consiste en intentar determinar el área de una región por medio de aproximaciones utilizando regiones poligonales cuya área sea más fácil de calcular, la idea es continuar con el proceso aumentando los lados de los polígonos hasta llegar a la mejor aproximación posible de la región que queremos determinar. Este método fue usado satisfactoriamente por Arquímedes (287-212 A.C.) para hallar fórmulas exactas de las áreas del círculo y de algunas otras figuras especiales. En la siguiente figura podemos ver al método de exhaución aplicado para determinar el área del círculo.

Método exhaustivo para hallar el área del círculo

Desde Arquímedes, gradualmente, el método de exhaución fue transformándose en lo que hoy se conoce como Cálculo integral, nueva y potente disciplina que, como ya mencionamos, tiene numerosas aplicaciones no sólo en problemas relativos a áreas y volúmenes, sino también en problemas de otras ciencias. El Cálculo integral, que mantiene alguno de los caracteres originales del método de exhaución, recibió su mayor impulso en el siglo XVII, debido a los esfuerzos de Isaac Newton (1642-1727) y Gottfried Leibniz (1646-1716), y su desarrollo continuó durante el siglo XIX, hasta que Augustin-Louis Cauchy (1789-1857) y Bernhard Riemann (1826-1866) le dieron una base matemática firme.

Funciones

Las Funciones son los objetos fundamentales con los que tratamos en el Cálculo. Las mismas pueden ser representadas de diferentes maneras: por una ecuación, en una tabla, por un gráfico, o en palabras. Se utilizan principalmente como modelos matemáticos para representar fenómenos del mundo real.

La palabra Función fue introducida en las Matemáticas por Leibniz, quien utilizaba este término para designar cierto tipo de fórmulas matemáticas. Una Función surge cada vez que una cantidad depende de otra. Más precisamente la definición de Función es esencialmente la siguiente: Dados dos conjuntos de objetos, el conjunto X y el conjunto Y, una Función es una regla que asocia a cada objeto de X, uno y sólo un, objeto en Y. El conjunto X se denomina el dominio de la Función. Los objetos de Y, asociados con los objetos en X forman otro conjunto denominado el recorrido de la Función. Generalmente se utilizan las letras $f, g, h, G$ y $H$ para designarlas. Si $f$ es una función dada y $x$ es un objeto de su dominio, la notación $f (x)$ se utiliza para designar el objeto que en el recorrido corresponde a $x$ , en la Función $f$ , y se denomina el valor de la función $f$ en $x$ . El símbolo $f (x)$ se lee, «f de x».

Muchas veces resulta útil pensar en una Función como si fuera una máquina. Si $x$ está en el dominio de la función $f$ , entonces cuando $x$ entra en la máquina, se acepta como una entrada y la máquina produce una salida $f (x)$ de acuerdo a la regla de la función. Así, podemos pensar al dominio como el conjunto de todas las entradas posibles y al recorrido como el conjunto de todas las salidas posibles.

El método más común para la visualización de una Función es su gráfica. Si $f$ es una Función con dominio $D$ , a continuación, su gráfica es el conjunto de pares ordenados.

{(x, f (x)) ∣ x \in D}

Aquí debemos tener en cuenta que el par $(x, f (x))$ , es un par entrada-salida, el valor de $x$ representa el valor de entrada, mientras que el valor de $f (x)$ representa la salida de la Función. En otras palabras, la gráfica de $f$ se compone de todos puntos $(x, y)$ en el plano de coordenadas tal que $y = f (x)$ y $x$ está en el dominio de $f$ . La gráfica de una Función $f$ nos da una imagen útil del comportamiento o la “historia de vida” de la misma.

Gráfica de funciones

Funciones con Python

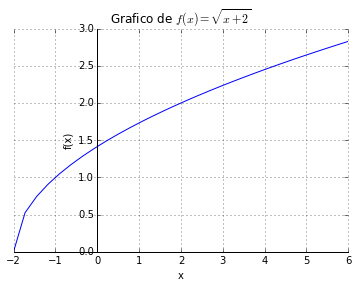
Para definir las Funciones en Python utilizamos la instrucción def. Así por ejemplo si quisiéramos definir a la Función $f (x) = \sqrt{x + 2}$ dentro de Python, lo podríamos hacer de la siguiente forma:

import numpy as np

def f(x):
    return np.sqrt(x + 2)

En este ejemplo, primero estamos importando la librería numpy, para trabajar más fácilmente con vectores, los cuales simplifican los cálculos numéricos. Luego utilizamos la instrucción def para definir la función, que este caso se va a llamar f y va a tener como único parámetro al objeto x. Esta función nos va a devolver el valor de la raíz cuadrada de $x + 2$ . Ahora, si por ejemplo quisiéramos saber los valores de la función $f (x)$ para los $x, - 2, - 1, 0, 2, 4$ y $6$ . podríamos invocar a esta función de la siguiente manera:

x = np.array([-2, -1, 0, 2, 4, 6])  # Creando el vector de valores de x
y = f(x)
y

array([ 0.        ,  1.        ,  1.41421356,  2.        ,  2.44948974,
        2.82842712])

Si quisiéramos verlo en forma de tabla, podemos ayudarnos de la librería pandas y su estructura de datos DataFrame, la cual tiene una forma tabular.

import pandas as pd

tabla = pd.DataFrame( list(zip(x, y)), columns=['x', 'f(x)'] )
tabla

	x	f(x)
0	-2	0.000000
1	-1	1.000000
2	0	1.414214
3	2	2.000000
4	4	2.449490
5	6	2.828427

Por último, si quisiéramos graficar funciones con Python, podemos utilizar la librería Matplotlib, y pasarle los valores de $x$ e $y$ al método plot del objeto pyplot.

%matplotlib inline

import matplotlib.pyplot as plt

def move_spines():
    """Esta funcion divide pone al eje y en el valor
    0 de x para dividir claramente los valores positivos y
    negativos."""
    fix, ax = plt.subplots()
    for spine in ["left", "bottom"]:
        ax.spines[spine].set_position("zero")

    for spine in ["right", "top"]:
        ax.spines[spine].set_color("none")

    return ax

x = np.linspace(-2, 6, num=30)

ax = move_spines()
ax.grid()
ax.plot(x, f(x))
plt.title(r"Grafico de $f(x)=\sqrt{x + 2}$")
plt.ylabel('f(x)')
plt.xlabel('x')
plt.show()

png

Límites

Uno de los conceptos más importantes dentro del Cálculo es el concepto de Límite. Se dice que una función $f$ tiende hacia el Límite $l$ cerca de $a$ , si se puede hacer que $f (x)$ este tan próxima como queramos de $l$ , haciendo que $x$ esté suficientemente cerca de $a$ , pero siendo distinta de $a$ . Así por ejemplo si analizamos la función $f (x) = x^{2} - x + 2$ , para los valores cercanos a 2, podríamos ver los siguientes resultados.

Ver Código

# <!-- collapse=True -->
def f(x):
    return x**2 - x + 2

x = np.array([1, 1.5, 1.9, 1.95, 1.99, 1.999, 2.001, 2.05, 2.1, 2.2, 2.5, 3 ])
y = f(x)
tabla = pd.DataFrame(list(zip(x, y)), columns=['x', 'f(x)'])
tabla

	x	f(x)
0	1.000	2.000000
1	1.500	2.750000
2	1.900	3.710000
3	1.950	3.852500
4	1.990	3.970100
5	1.999	3.997001
6	2.001	4.003001
7	2.050	4.152500
8	2.100	4.310000
9	2.200	4.640000
10	2.500	5.750000
11	3.000	8.000000

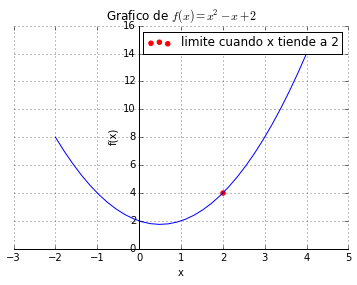
de acuerdo con esta tabla, podemos ver que a medida que hacemos al valor de $x$ cercano a 2, vemos que $f (x)$ se hace muy cercana a 4. Incluso podríamos hacer a $f (x)$ tan cercana como queramos a 4, haciendo que $x$ este lo suficientemente cerca de 2. Por lo tanto, podemos expresar esta propiedad diciendo que el "Límite de la función $f (x) = x^{2} - x + 2$ cuando $x$ se acerca a 2 es igual a 4." y lo podemos representar con la siguiente notación:

lim_{x \to 2} (x^{2} - x + 2) = 4

Gráficamente lo podemos ver del siguiente modo.

Ver Código

# <!-- collapse=True -->
x = np.linspace(-2, 4, num=30)

ax = move_spines()
ax.grid()
ax.plot(x, f(x))
ax.scatter(2, 4, label="limite cuando x tiende a 2", color='r')
plt.legend()
plt.title(r"Grafico de $f(x)=x^2 -x + 2$")
plt.ylabel('f(x)')
plt.xlabel('x')
plt.show()

png

Las leyes de los límites

Calcular el valor exacto de los Límites muchas veces no suele tan fácil como reemplazar el valor de $a$ en $f (x)$ . Es por esto que es importante conocer algunas propiedades de los Límites, ellas son:

Ley de la suma: El límite de la suma de dos funciones es la suma de sus límites.
Ley de la diferencia: El límite de la diferencia de dos funciones es la diferencia de sus límites.
Ley del producto: El límite del producto de dos funciones es el producto de sus límites.
ley del múltiplo constante: El límite de una constante por una función es la constante por el límite de la función.
Ley del cociente: El límite del cociente de dos funciones es el cociente de sus límites, siempre que el límite del denominador sea diferente de cero.

Es decir que si tenemos a la constante $C$ y a los límites $lim_{x \to a} f (x)$ y $lim_{x \to a} g (x)$ . Entonces podemos expresar estas propiedades matemáticamente de la siguiente forma:

1- Ley de la suma: $lim_{x \to a} [f (x) + g (x)] = lim_{x \to a} f (x) + lim_{x \to a} g (x)$ .

2- Ley de la diferencia: $lim_{x \to a} [f (x) - g (x)] = lim_{x \to a} f (x) - lim_{x \to a} g (x)$ .

3- Ley del producto: $lim_{x \to a} [f (x) \cdot g (x)] = lim_{x \to a} f (x) \cdot lim_{x \to a} g (x)$ .

4- ley del multiplo constante: $lim_{x \to a} [C \cdot f (x)] = C \cdot lim_{x \to a} f (x)$ .

5- Ley del cociente: $lim_{x \to a} [\frac{f (x)}{g (x)}] = \frac{lim_{x \to a} f (x)}{lim_{x \to a} g (x)}$ , si $lim_{x \to a} g (x) \neq 0$ .

Calculando Límites con Python

Con Python, podemos resolver Límites fácilmente utilizando la librería SymPy, la cual nos proporciona el objeto Limit para representarlos en Python. Su sintaxis es la siguiente: Limit(función, variable, punto). Entonces para calcular el límite de $f (x)$ cuando $x$ tiende a 0, debemos escribir:

Limit(f(x), x, 0)

Lo utilizamos de la siguiente forma:

from sympy.interactive import printing
from sympy import Limit, limit, Symbol, S

# imprimir con notación matemática.
printing.init_printing(use_latex='mathjax')

x = Symbol('x') # Creando el simbolo x.
Limit(x**2 - x + 2, x, 2) # Creando el objeto Limit

lim_{x \to 2^{+}} (x^{2} - x + 2)

# Resolviendo el Limite con el metodo doit()
Limit(x**2 - x + 2, x, 2).doit()

4

# La funcion limit nos da directamente el resultado
limit(x**2 - x + 2, x, 2)

4

# Resolviendo limite 1/x cuando x tiende a infinito
Limit(1/x, x, S.Infinity)

lim_{x \to \infty} \frac{1}{x}

Limit(1/x, x, S.Infinity).doit()

0

Como vemos, primero creamos el símbolo para representar a la variable x utilizando el objeto Symbol, y luego creamos nuestro límite utilizando el objeto Limit. Por último para resolver el límite, simplemente llamamos al método doit() sobre el objeto Limit que acabamos de crear. También podemos calcular los Límites de valores de $x$ que tiendan hacia el infinito utilizando la clase especial S.Infinity que nos proporciona SymPy.

Ahora que ya conocemos que es una Función y que es un Límite, ya estamos en condiciones de adentrarnos en el Cálculo diferencial y analizar el concepto de Derivada.

Derivadas

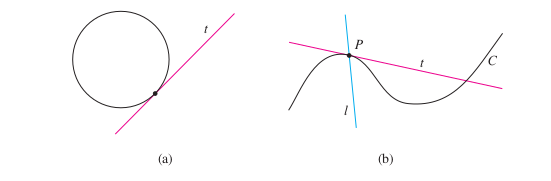
Para poder comprender el concepto de Derivada primero debemos abordar el problema de la recta tangente a un curva. La palabra tangente se deriva de la palabra griega Tangens, que significa “que toca”. Así una tangente a una curva es una línea que toca la curva. En otras palabras, una línea tangente debe tener la misma dirección que la curva en el punto de contacto. Para un círculo podríamos simplemente seguir la definición de Euclides y decir que la tangente es una línea que cruza el círculo una y sólo una vez (ver figura a). Pero para curvas más complicadas este definición es inadecuada. Por ejemplo en la figura b podemos ver dos líneas $l$ y $t$ que pasan por el punto $P$ en una curva $C$ . La línea $l$ cruza a la curva $C$ sólo una vez, pero ciertamente no se parece a lo que pensamos como una tangente. La línea $t$ , en cambio, se parece a una tangente pero intercepta a $C$ dos veces.

El problema de la tangente

El intento de resolver este problema fue lo que condujo a Fermat a descubrir algunas de las ideas rudimentarias referentes a la noción de Derivada. Aunque la derivada se introdujo inicialmente para el estudio del problema de la tangente, pronto se vio que proporcionaba también un instrumento para el cálculo de velocidades y, en general para el estudio de la variación o tasa de cambio de una función.

La Derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función, según cambie el valor de su variable independiente. La Derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio medio de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado. Entonces el valor de la Derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de Derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.

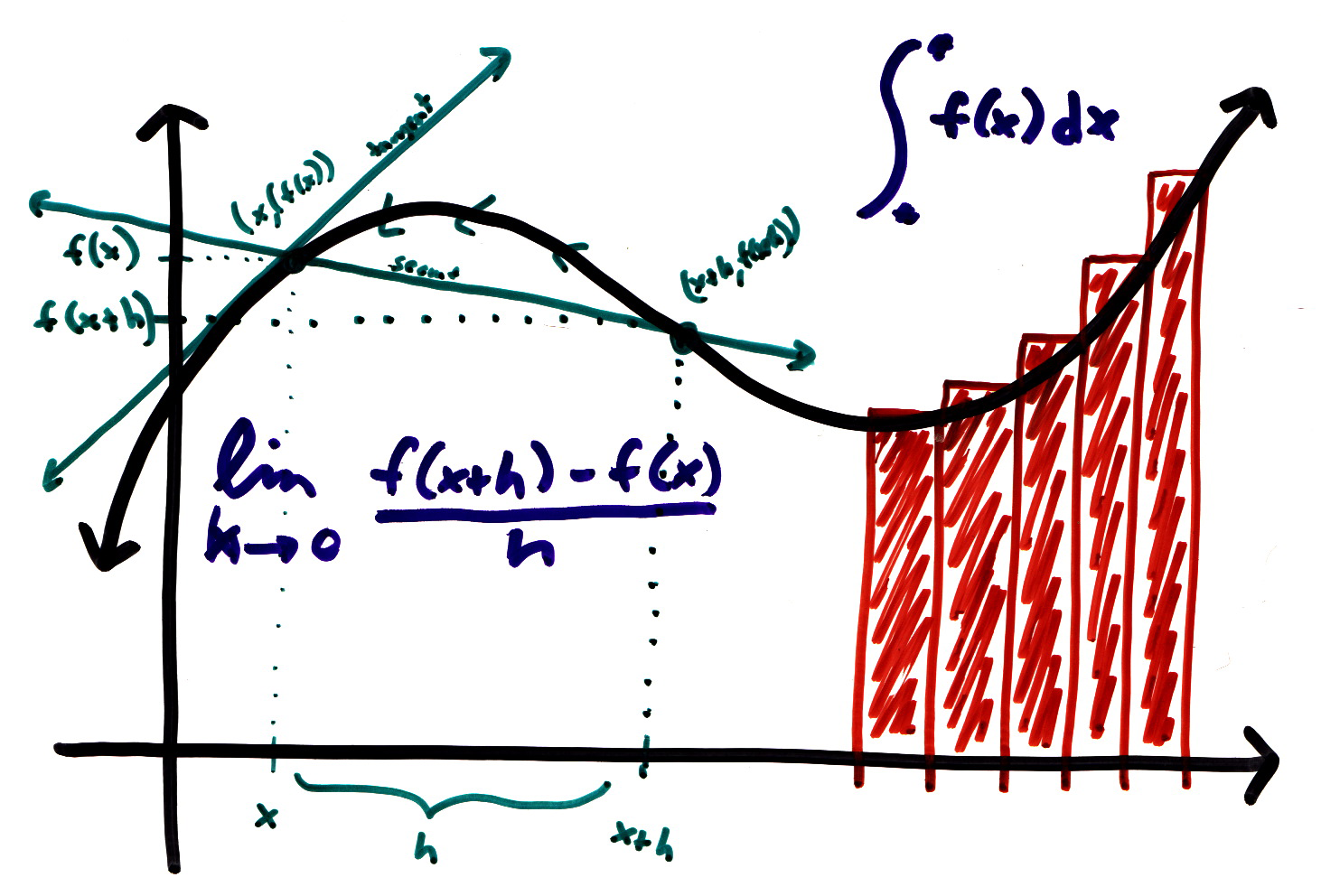
Matemáticamente, la Derivada es una caso especial de Límite, el cual surge cada vez que queremos calcular la pendiente de la recta tangente o la velocidad de cambio de un objeto. Éste Límite ocurre tan frecuentemente que se le ha da un notación y un nombre determinados. Así la Derivada de una función $f$ en el punto a, representada por $f^{'} (a)$ , es:

f^{'} (a) = lim_{h \to 0} \frac{f (a + h) - f (a)}{h}

donde $h$ representa la variación de $a$ . Esta misma definición, puede ser representada también del siguiente modo, utilizando la notación de Leibniz.

\frac{d y}{d x} = lim_{d x \to 0} \frac{f (x + d x) - f (x)}{d x}

Así, por ejemplo si quisiéramos saber cuál es la Derivada de la función $f (x) = x^{3}$ , podemos aplicar la definición anterior del siguiente modo.

Comenzamos, definiendo a $f (x + d x) = (x + d x)^{3}$ , luego expandimos a:

(x + d x)^{3} = f (x + d x) = x^{3} + 3 x^{2} d x + 3 x d x^{2} + d x^{3}

Luego reemplazamos esta función en nuestra definición de Derivada:

\frac{d x}{d y} = \frac{x^{3} + 3 x^{2} d x + 3 x d x^{2} + d x^{3} - x^{3}}{d x}

Simplificamos los términos:

\frac{d x}{d y} = \frac{3 x^{2} d x + 3 x d x^{2} + d x^{3}}{d x} \Rightarrow 3 x^{2} + 3 x d x + d x^{2}

y cuando $d x$ tiende a cero, obtenemos finalmente la función Derivada:

\frac{d}{d x} x^{3} = 3 x^{2}

Reglas de Derivación

Si fuera siempre necesario calcular las Derivadas directamente de la definición, como hicimos anteriormente, éstos cálculos podrían ser tediosos y complicados. Afortunadamente, varias reglas se han desarrollado para encontrar Derivadas sin tener que usar la definición directamente. Estas fórmulas simplifican enormemente la tarea de la diferenciación y se conocen como reglas de derivación. Algunas de ellas son las siguientes:

Funciones comunes	Función original	Función Derivada
Constantes	$c$	0
	$x$	1
Cuadrado	$x^{2}$	$2 x$
Raiz cuadrada	$\sqrt{x}$	$\frac{1}{2} x^{- \frac{1}{2}}$
Exponenciales	$e^{x}$	$e^{x}$
	$a^{x}$	$a^{x} (\ln a)$
Logaritmicas	$\ln x$	$\frac{1}{x}$
	$\log_{a} x$	$\frac{1}{x \ln a}$
Trigonométricas	$\sin x$	$\cos x$
	$\cos x$	$- \sin x$
	$\tan x$	$\sec^{2} (x)$
Trigonométricas inversas	$\sin^{- 1} (x)$	$\frac{1}{\sqrt{1 - x^{2}}}$
	$\cos^{- 1} (x)$	$\frac{- 1}{\sqrt{1 - x^{2}}}$
	$\tan^{- 1} (x)$	$\frac{1}{1 - x^{2}}$

1- Regla de la función de grado n: Esta regla nos dice que una función de grado n, donde n es un exponente real, se representa por $f (x) = x^{n}$ y su derivada es $f^{'} (x) = n x^{n - 1}$ . Así por ejemplo, si quisiéramos saber la derivada de $f (x) = x^{5}$ , aplicando la regla obtenemos, $f^{'} (x) = 5 x^{5 - 1} \Rightarrow 5 x^{4}$ .

2- Regla de la multiplicación por una constante: Esta regla establece que una función con la forma $f (x) = C x$ , donde $C$ es una constante; entonces la derivada de esta función va a ser igual a: $f^{'} (x) = C x^{'}$ ; es decir a la constante por la derivada de $x$ . Así por ejemplo si tenemos la función $f (x) = 5 x^{3}$ , primero debemos a obtener la derivada de $x^{3}$ , la cual aplicando la regla anterior sabemos que es $3 x^{2}$ y luego a esta derivada la multiplicamos por la constante 5, para obtener el resultado final $f^{'} (x) = 15 x^{2}$ .

3- Regla de la suma: Esta regla establece que la derivada de la suma de dos funciones es igual a la suma de las derivadas de cada una de ellas. Es decir, $(f + g)^{'} (x) = f^{'} (x) + g^{'} (x)$ . Así por ejemplo la derivada de la función $f (x) = 5 x^{3} + x^{2}$ va a ser igual a $f^{'} (x) = 15 x^{2} + 2 x$ .

4- Regla de la diferencia: Esta regla establece que la derivada de la diferencia entre dos funciones es igual a la diferencia entre las derivadas de cada una de ellas. Es decir, $(f - g)^{'} (x) = f^{'} (x) - g^{'} (x)$ . Así por ejemplo la derivada de la función $f (x) = 5 x^{3} - x^{2}$ va a ser igual a $f^{'} (x) = 15 x^{2} - 2 x$ .

5- Regla del producto: Esta regla establece que la derivada de un producto de dos funciones es equivalente a la suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función sin derivar. Es decir, $(f \cdot g)^{'} = f^{'} \cdot g + f \cdot g^{'}$ . Así por ejemplo si quisiéramos derivar la función $h (x) = (2 x + 1) (x^{3} + 2)$ , primero obtenemos las derivadas de cada termino, $f^{'} (x) = 2$ y $g^{'} (x) = 3 x^{2}$ y luego aplicamos la formula $h^{'} (x) = 2 (x^{3} + 2) + (2 x + 1) 3 x^{2}$ , los que nos da un resultado final de $h^{'} (x) = 8 x^{3} + 3 x^{2} + 4$ .

6- Regla del cociente: Esta regla establece que la derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado. Es decir, ${(\frac{f}{g})}^{'} = \frac{f^{'} g - f g^{'}}{g^{2}}$ . Por ejemplo, para obtener la derivada de la función $h (x) = \frac{3 x + 1}{2 x}$ , aplicando la formula obtenemos que $h^{'} (x) = \frac{3 \cdot (2 x) - (3 x + 1) \cdot 2}{2 x^{2}}$ , y simplificando llegamos al resultado final de $h^{'} (x) = - \frac{1}{2 x^{2}}$ .

7- Regla de la cadena: La regla de la cadena es una fórmula para calcular la derivada de la composición de dos o más funciones. Esto es, si $f$ y $g$ son dos funciones, entonces la regla de la cadena expresa la derivada de la función compuesta $f (g (x))$ en términos de las derivadas de $f$ y $g$ . Esta derivada va a ser calculada de acuerdo a la siguiente formula: $f^{'} (g (x)) = f^{'} (g (x)) \cdot g^{'} (x)$ . Por ejemplo, si quisiéramos saber la derivada de la función $h (x) = \sin (x^{2})$ , aplicando la formula obtenemos que $h^{'} (x) = \cos (g (x)) \cdot 2 x$ , lo que es igual a $h^{'} (x) = 2 x \cos (x^{2})$ .

Derivadas de mayor orden

Si tenemos una función $f$ , de la cual podemos obtener su derivada $f^{'}$ , la cual también es otra función que podemos derivar, entonces podemos obtener la derivada de segundo orden de $f$ , la cual representaremos como $f^{″}$ . Es decir, que la derivada de segundo orden de $f$ , va a ser igual a la derivada de su derivada. Siguiendo el mismo proceso, podemos seguir subiendo en la jerarquía y obtener por ejemplo, la tercer derivada de $f$ . Utilizando la notación de Leibniz, expresaríamos a la segunda derivada del siguiente modo:

\frac{d}{d y} (\frac{d y}{d x}) = \frac{d^{2} y}{d x^{2}}

Calculando Derivadas con Python

Con Python, podemos resolver Derivadas utilizando nuevamente la librería SymPy. En este caso, ahora vamos a utilizar el objeto Derivative. Su sintaxis es la siguiente: Derivative(funcion, variable, orden de derivación). Lo utilizamos de la siguiente forma:

from sympy import Derivative, diff, simplify

fx = (2*x + 1)*(x**3 + 2)
dx = Derivative(fx, x).doit()
dx

2 x^{3} + 3 x^{2} (2 x + 1) + 4

# simplificando los resultados
simplify(dx)

8 x^{3} + 3 x^{2} + 4

# Derivada de segundo orden con el 3er argumento.
Derivative(fx, x, 2).doit()

6 x (4 x + 1)

# Calculando derivada de (3x +1) / (2x)
fx = (3*x + 1) / (2*x)
dx = Derivative(fx, x).doit()
simplify(dx)

- \frac{1}{2 x^{2}}

# la función diff nos da directamente el resultado
simplify(diff(fx, x))

- \frac{1}{2 x^{2}}

# con el metodo subs sustituimos el valor de x
# para obtener el resultado numérico. Ej x = 1.
diff(fx, x).subs(x, 1)

- \frac{1}{2}

Como podemos ver, el método para calcular las Derivadas con Python, es muy similar al que vimos anteriormente al calcular los Límites. En el ejemplo, también utilizamos la función simplify, la cual nos ayuda a simplificar los resultados; y el método subs para sustituir el valor de $x$ y obtener el resultado numérico.

Ahora que ya conocemos al Cálculo diferencial, es tiempo de pasar hacia la otra rama del Cálculo, el Cálculo integral, y analizar el concepto de Integración.

Integrales

La idea de Integral es el concepto básico del Cálculo integral. Pero para poder comprender este concepto, primero debemos abordar el problema del área. Como bien sabemos, el área es una medida de la extensión de una superficie. Determinar esta medida para superficies con líneas rectas, suele ser bastante fácil. Por ejemplo para un rectángulo, su área se define como el producto de la longitud y el ancho. O para un triángulo como la mitad de la base por la altura. El área de cualquier otro polígono se encuentra al dividirlo en triángulos y luego sumar las áreas de cada uno ellos. Pero para los casos de las regiones con líneas curvas, el cálculo del área ya no suele ser tan fácil. Para estos casos debemos recurrir a un método similar al de exhaución que mencionábamos en la introducción del artículo. Es decir, que vamos a ir dividiendo la región en varios rectángulos de $Δ x$ de ancho y luego podemos ir calculando el área como la suma del las áreas de cada uno de estos rectángulos. A medida que vamos agregando más rectángulos, haciendo $Δ x$ cada vez más pequeño, nos vamos aproximando cada vez más al valor real del área de la superficie curva. Hasta el punto de que, cuando $Δ x$ tiende a cero, podemos alcanzar el resultado exacto del área de nuestra superficie curva. Es decir, que realizando una suma de infinitamente más angostos rectángulos, podemos determinar el resultado exacto del área de nuestra superficie curva. Este proceso lo podemos ver más claramente en la siguiente figura.

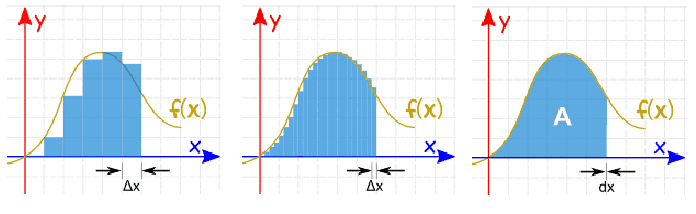
Como vemos, al igual que pasaba con el caso de las Derivadas, al querer calcular el área de una superficie curva, nos encontramos ante un caso especial de Límite (aquí vemos también por qué el concepto de Límite es tan importante para el Cálculo!). Este tipo de Límite surge en una amplia variedad de situaciones, no solo al calcular áreas, sino que también lo podemos encontrar al calcular la distancia recorrida por un objeto o el volumen de un sólido. Por lo tanto, se le ha dado una notación y un nombre determinado. De esta forma la definición matemática de la Integral definida, sería la siguiente:

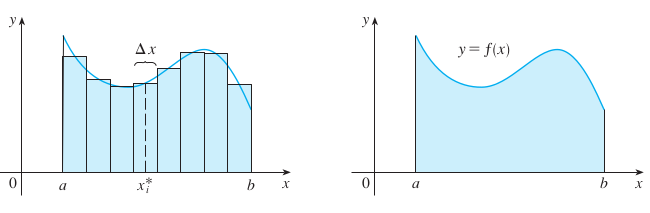
Si $f$ es una función definida por $a ⩽ x ⩽ b$ , podemos dividir el intervalo $[a, b]$ en $n$ subintervalos de $Δ x (b - a) / n$ de ancho. Dónde $x_{0} (= a), x_{1}, x_{2}, \dots, x_{n} (= b)$ serán los puntos finales de estos subintervalos y $x_1^, x_2^, \dots, x_n^$, serán puntos intermedios en estos subintervalos, de tal forma que $x_i^$ se encuentre en el k-simo subintervalo $[x_{i - 1}, x_{i}]$ . Entonces la Integral definida de $f$ entre $a$ y $b$ , es:

\int_{a}^{b} f (x) d x = lim_{n \to \infty} \sum_{i = 1}^{n} f (x_{i}^{*}) Δ x

El símbolo de la Integral, $\int$ , fue introducido por Leibniz, viene a ser una “S” alargada y fue elegido ya que la Integral es en definitiva un Límite de sumas infinitesimales. En esta notación, $a$ y $b$ son los límites de la integración y $d x$ indica que $x$ es la variable independiente. La suma:

\sum_{i = 1}^{n} f (x_{i}^{*}) Δ x

que vemos en la definición, es conocida como la suma de Reimann, en honor al matemático alemán Bernhard Reimann que la desarrolló.

Integrales definidas e indefinidas

Una distinción importante que debemos hacer al hablar de Integrales, es la diferencia entre una Integral definida y una integral indefinida o antiderivada. Mientras que la Integral definida, que representamos con el símbolo, $\int_{a}^{b} f (x) d x$ , es un número, un resultado preciso de la medida de un área, distancia o volumen; la integral indefinida, que representamos como, $\int f (x) d x$ , es una función o familia de funciones. Más adelante, cuando hablemos del teorema fundamental del cálculo, veremos por qué esta distinción es tan importante. Pero antes, veamos como podemos hacer para calcular Integrales.

Reglas de integración

Cómo podemos ver de la definición que dimos de Integrales, estas parecen sumamente complicadas de calcular. Por suerte, al igual que para el caso de Derivadas, existen varias reglas que podemos utilizar para poder calcular las integrales indefinidas, en forma más sencilla. Algunas de ellas son:

Funciones comunes	Función original	Integral indefinida ( $C$ es una constante)
Constante	$\int a d x$	$a x + C$
Variable	$\int x d x$	$\frac{x^{2}}{2} + C$
Cuadrado	$\int x^{2} d x$	$\frac{x^{3}}{3} + C$
Reciproca	$\int (\frac{1}{x}) d x$	\(\ln
Exponenciales	$\int e^{x} d x$	$e^{x} + C$
	$\int a^{x} d x$	$\frac{a^{x}}{\ln (a)} + C$
	$\int \ln (x) d x$	$x \ln (x) - x + C$
Trigonométricas	$\int \sin (x) d x$	$- \cos (x) + C$
	$\int \cos (x) d x$	$\sin (x) + C$
	$\int \sec^{2} (x) d x$	$\tan (x) + C$

1- Regla de la función de grado n: Esta regla nos dice que una función de grado n, donde n es un exponente real distinto de -1, se representa por $f (x) = x^{n}$ y su integral es $\int x^{n} d x = \frac{x^{n + 1}}{n + 1} + C$ . Así por ejemplo, si quisiéramos saber la integral de $f (x) = x^{3}$ , aplicando la regla obtenemos, $\int x^{3} d x = \frac{x^{4}}{4} + C$ .

2- Regla de la multiplicación por una constante: Esta regla establece que una función con la forma $f (x) = C x$ , donde $C$ es una constante; entonces la integral de esta función va a ser igual a: $\int C x d x = C \int x d x$ ; es decir a la constante por la integral de $x$ . Así por ejemplo si tenemos la función $f (x) = 4 x^{3}$ , primero debemos a obtener la integral de $x^{3}$ , la cual aplicando la regla anterior sabemos que es $\int x^{3} d x = \frac{x^{4}}{4} + C$ y luego a esta integral la multiplicamos por la constante 4, para obtener el resultado final $\int 4 x^{3} d x = x^{4} + C$ .

3- Regla de la suma: Esta regla establece que la integral de la suma de dos funciones es igual a la suma de las integrales de cada una de ellas. Es decir, $\int (f + g) d x = \int f d x + \int g d x$ . Así por ejemplo la integral de la función $f (x) = 4 x^{3} + x^{2}$ va a ser igual a $\int (4 x^{3} + x^{2}) d x = x^{4} + \frac{x^{3}}{3} + C$ .

4- Regla de la diferencia: Esta regla establece que la integral de la diferencia entre dos funciones es igual a la diferencia entre las integrales de cada una de ellas. Es decir, $\int (f - g) d x = \int f d x - \int g d x$ . Así por ejemplo la integral de la función $f (x) = 4 x^{3} - x^{2}$ va a ser igual a $\int (4 x^{3} - x^{2}) d x = x^{4} - \frac{x^{3}}{3} + C$ .

En todos estos ejemplos, podemos ver la aparición de una misteriosa constante $C$ , esta es la que se conoce como constante de integración. Esta constante expresa una ambigüedad inherente a la construcción de las integrales. Es por esta ambigüedad que cuando hablamos de la integral indefinida decimos que expresa una familia de funciones $f (x) + C$ .

Teorema fundamental del Cálculo

El teorema fundamental del cálculo establece una conexión entre las dos ramas del Cálculo: el Cálculo diferencial y el Cálculo integral. Como ya hemos visto, el Cálculo diferencial surgió del problema de la tangente , mientras que el Cálculo integral surgió de un problema aparentemente sin relación con este, el problema del área. Fue Isaac Barrow, quien descubrió que estos dos problemas están en realidad estrechamente relacionados. De hecho, se dio cuenta de que la derivación y la integración son procesos inversos. El teorema fundamental del cálculo nos da la relación inversa precisa entre la Derivada y la Integral. Fueron Newton y Leibniz quienes aprovecharon esta relación y la utilizaron para desarrollar el Cálculo. En particular, vieron que esta relación les permitía calcular áreas e Integrales con mucha facilidad y sin tener que calcularlas como límites de sumas. Es decir, que si tomamos una función $f$ , y obtenemos primero su Derivada, y luego calculamos la Integral sobre esta función Derivada $f^{'} (x)$ . Obtenemos nuevamente función original $f$ . Lo que una hace, la otra lo deshace. El teorema fundamental del cálculo es sin duda el teorema más importante en el Cálculo y, de hecho, se ubica como uno de los grandes logros de la mente humana. Matemáticamente, este teorema se suele dividir en dos partes y nos dice lo siguiente:

Teorema fundamental del Calculo, parte 1. si $f$ es una función continua en el intervalo $[a, b]$ , entonces la función $g$ definida como:

g (x) = \int_{a}^{x} f (t) d t a ⩽ x ⩽ b

es continua en el intervalo $[a, b]$ y diferenciable en $(a, b)$ , y $g^{'} (x) = f (x)$ .

Teorema fundamental del Calculo, parte 2. si $f$ es una función continua en el intervalo $[a, b]$ , entonces:

\int_{a}^{b} f (x) d x = F (b) - F (a)

en donde $f$ es la antiderivada de $f$ , o sea, una función tal que F’ = f.

En definitiva, lo que nos dice la primera parte es que las operaciones de derivación y de integración son operaciones inversas. La segunda parte nos proporciona un método para calcular integrales definidas, en base a la antiderivada o integral indefinida.

Así, por ejemplo, si quisiéramos calcular la Integral:

\int_{0}^{3} (x^{3} - 6 x) d x

primero obtenemos su integral indefinida.

\int (x^{3} - 6 x) d x = \frac{x^{4}}{4} - 6 \frac{x^{2}}{2}

y por último aplicamos la segunda parte del teorema fundamental del cálculo para obtener la integral definida en $[0, 3]$ , reemplazando estos valores en la integral indefinida que acabamos de obtener.

\int_{0}^{3} (x^{3} - 6 x) d x = (\frac{1}{4} \cdot 3^{4} - 3 \cdot 3^{2}) - (\frac{1}{4} \cdot 0^{4} - 3 \cdot 0^{2}) = - \frac{27}{4}

Calculando Integrales con Python

Con Python, podemos resolver Integrales con la ayuda de la, en este punto ya invaluable, librería SymPy. En este caso, vamos a utilizar el objeto Integral. Su sintaxis es la siguiente: Integral(funcion, variable). Lo utilizamos de la siguiente forma:

from sympy import Integral, integrate

fx = x**3 - 6*x
dx = Integral(fx, x).doit()
dx

\frac{x^{4}}{4} - 3 x^{2}

# la función integrate nos da el mismo resultado
integrate(fx, x)

\frac{x^{4}}{4} - 3 x^{2}

El objeto Integral también nos permite calcular integrales definidas. En este caso, en el segundo argumento le pasamos una tupla cuyo primer elemento es la variable de integración, su segundo elemento es el límite inferior de integración y el último es el límite superior.

# Calculando integral definida para [0, 3]
Integral(fx, (x, 0, 3)).doit()

- \frac{27}{4}

# Comprobando Teorema fundamental del calculo.
# Integración y diferenciacion son operaciones inversas.
diff(integrate(fx))

x^{3} - 6 x

integrate(diff(fx))

x^{3} - 6 x

Como podemos ver, el método para calcular las Integrales con Python, es muy similar a lo que ya veníamos utilizando al calcular Límites y Derivadas. Para calcular Integrales en forma numérica, también podemos recurrir al módulo scipy.integrate, el cual es muy útil para resolver ecuaciones diferenciales, pero eso ya va a quedar para otro artículo.

Con esto concluyo esta introducción por el fascinante mundo del Cálculo, espero lo hayan disfrutado tanto como yo!

Saludos!

Este post fue escrito utilizando Jupyter notebook. Pueden descargar este notebook o ver su version estática en nbviewer.

Introducción al Cálculo con Python

Introducción#

Historia#

Funciones#

Funciones con Python#

Límites#

Las leyes de los límites#

Calculando Límites con Python#

Derivadas#

Reglas de Derivación#

Derivadas de mayor orden#

Calculando Derivadas con Python#

Integrales#

Integrales definidas e indefinidas#

Reglas de integración#

Teorema fundamental del Cálculo#

Calculando Integrales con Python#