Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Matemáticas, análisis de datos y python. El contenido esta bajo la licencia BSD.

Ecuaciones Diferenciales con python

Introducción

Vivimos en un mundo en constante cambio. La posición de la Tierra cambia con el tiempo; la velocidad de un objeto en caída libre cambia con la distancia; el área de un círculo cambia según el tamaño de su radio; la trayectoria de un proyectil cambia según la velocidad y el ángulo de disparo. Al intentar modelar matemáticamente cualquiera de estos fenómenos, veremos que generalmente adoptan la forma de una o más Ecuaciones diferenciales.

Nota: Antes de continuar leyendo, si no tienen frescos sus conocimientos básicos de Cálculo integral y Cálculo diferencial; les recomiendo que visiten mi anterior artículo de Introducción al Cálculo.

¿Qué es una ecuación diferencial?

Una Ecuación diferencial es una ecuación que involucra una variable dependiente y sus derivadas con respecto a una o más variables independientes. Muchas de las leyes de la naturaleza, en Física, Química, Biología, y Astronomía; encuentran la forma más natural de ser expresadas en el lenguaje de las Ecuaciones diferenciales. Estas ecuaciones no sólo tienen aplicaciones en la ciencias físicas, sino que también abundan sus aplicaciones en las ciencias aplicadas como ser Ingeniería, Finanzas y Economía.

Es fácil entender la razón detrás de esta amplia utilidad de las Ecuaciones diferenciales. Si recordamos que \(y = f(x)\) es una función, entonces su derivada \(dy / dx\) puede ser interpretada como el ritmo de cambio de \(y\) con respecto a \(x\). En muchos procesos naturales, las variables involucradas y su ritmo de cambio están conectados entre sí por medio de los principios científicos básicos que rigen el proceso. Cuando esta conexión es expresada matemáticamente, el resultado generalmente es una Ecuación diferencial.

Para ilustrar el caso, veamos un ejemplo. Según la segunda ley de la dinámica de Newton, la aceleración \(a\) de un cuerpo de masa \(m\) es proporcional a la fuerza total \(F\) que actúa sobre él. Si expresamos esto matemáticamente en la forma de una ecuación, entonces tememos que:

$$F = ma$$

A primera vista, esta ecuación no parece ser una Ecuación diferencial, pero supongamos que un objeto de masa \(m\) esta en caída libre bajo la influencia de la fuerza de gravedad. En este caso, la única fuerza actuando sobre el objeto es \(mg\), donde \(g\) es la aceleración debido a la gravedad. Si consideramos a \(u\), como la posición del objeto desde una altura determinada; entonces la velocidad de caída del objeto va a ser igual al ritmo de cambio de la posición \(u\) con respecto al tiempo \(t\); es decir que la velocidad es igual a \(v = du / dt\), o sea, la derivada de la posición del objeto con respecto al tiempo; y como la aceleración no es otra cosa que el ritmo de cambio de la velocidad, entonces podemos definir a la aceleración como una segunda derivada de la posición del objeto con respecto al tiempo, lo que es igual a decir que \(g = d^2u / dt^2\). De esta forma, podemos reescribir la ecuación inicial de la segunda ley de la dinámica de Newton como la siguiente Ecuación diferencial.

$$F = m\frac{d^2u}{dt^2}$$

De esta manera, estamos expresando a la segunda ley de la dinámica de Newton en función de la posición del objeto.

Ecuaciones diferenciales ordinarias y parciales

El caso precedente, es el caso típico de una Ecuación diferencial ordinaria, ya que todas las derivadas involucradas son tomadas con respecto a una única y misma variable independiente. Por otro lado, si en la ecuación tenemos derivadas de más de una variable independiente, debemos hablar de Ecuaciones difenciales parciales. Por ejemplo, si \(w = f(x, y, z, t)\) es una función de tiempo y 3 coordenadas de un punto en el espacio, entonces las siguientes son sus Ecuaciones diferenciales parciales:

$$ \begin{array} \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} = 0; \\ \\ a^2\left(\frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2}\right) = \frac{\partial w}{\partial t}; \\ \\ a^2\left(\frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2}\right) = \frac{\partial^2 w}{\partial t^2}. \end{array} $$

En esta caso, el símbolo \(\partial\), es la notación matemática para expresar que estamos derivando parcialmente, así por ejemplo, si queremos expresar que vamos a derivar z con respecto a x, escribimos \(\partial z / \partial x\).

Estos ejemplos, tienen una gran aplicación en Física y se conocen como la ecuación de Laplace, la ecuación del calor y la ecuación de onda respectivamente. En general, las Ecuaciones diferenciales parciales surgen en problemas de campos eléctricos, mecánica de fluidos, difusión y movimientos de ondas. La teoría de estas ecuaciones es bastante diferente con respecto a las ecuaciones diferenciales ordinarias y suelen ser también más complicadas de resolver. En este artículo me voy a enfocar principalmente en las ecuaciones diferenciales ordinarias, o EDOs para abreviar.

Orden de las Ecuaciones diferenciales

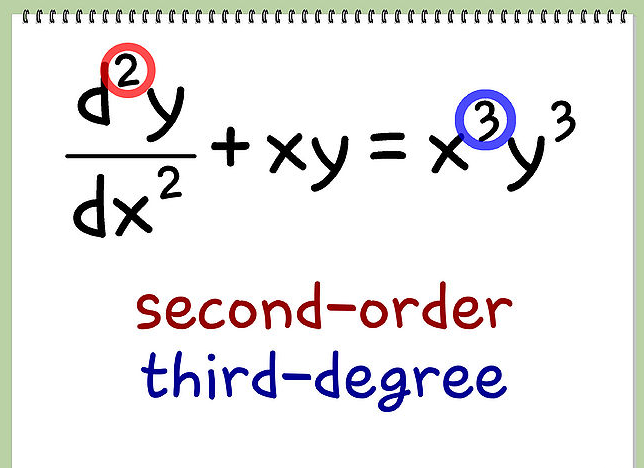
El orden de una Ecuación diferencial va a ser igual al orden de la mayor derivada presente. Así, en nuestro primer ejemplo, la Ecuación diferencial de la segunda ley de la dinámica de Newton es de segundo orden, ya que nos encontramos ante la segunda derivada de la posición del objeto con respecto al tiempo. La ecuación general de las ecuaciones diferenciales ordinarias de grado \(n\) es la siguiente:

$$F\left(x, y, \frac{dy}{dx}, \frac{d^2y}{dx^2}, \dots , \frac{d^ny}{dx^n}\right) = 0 $$

o utilizando la notación prima para las derivadas,

$$F(x, y, y', y'', \dots, y^{(n)}) = 0$$

La más simple de todas las ecuaciones diferenciales ordinarias es la siguiente ecuación de primer orden:

$$ \frac{dy}{dx} = f(x)$$

y para resolverla simplemente debemos calcular su integral indefinida:

$$y = \int f(x) dx + c$$

.

Ecuaciones diferenciales separables

Una ecuación separable es una ecuación diferencial de primer orden en la que la expresión para \(dx / dy\) se puede factorizar como una función de x multiplicada por una función de y. En otras palabras, puede ser escrita en la forma:

$$\frac{dy}{dx} = f(x)g(y)$$

El nombre separable viene del hecho de que la expresión en el lado derecho se puede “separar” en una función de \(x\) y una función de \(y\).

Para resolver este tipo de ecuaciones, podemos reescribirlas en la forma diferencial:

$$\frac{dy}{g(y)} = f(x)dx$$

y luego podemos resolver la ecuación original integrando:

$$\int \frac{dy}{g(y)} = \int f(x) dx + c$$

Éstas suelen ser las Ecuaciones diferenciales más fáciles de resolver, ya que el problema de resolverlas puede ser reducido a un problema de integración; a pesar de que igualmente muchas veces estas integrales pueden ser difíciles de calcular.

Ecuaciones diferenciales lineales

Uno de los tipos más importantes de Ecuaciones diferenciales son las Ecuaciones diferenciales lineales. Este tipo de ecuaciones son muy comunes en varias ciencias y tienen la ventaja de que pueden llegar a ser resueltas en forma analítica ya que su ecuación diferencial de primer orden adopta la forma:

$$\frac{dy}{dx} + P(x)y = Q(x) $$

donde, \(P\) y \(Q\) son funciones continuas de \(x\) en un determinado intervalo. Para resolver este tipo de ecuaciones de la forma \( y’ + P(x)y = Q(x)\), debemos multiplicar los dos lados de la ecuación por el factor de integración \(e^{\int P(x) dx}\) y luego integrar ambos lados. Así, si por ejemplo quisiéramos resolver la siguiente Ecuación diferencial:

$$\frac{dy}{dx} + 3x^2y = 6x^2$$

Primero calculamos el factor de integración, \(I(x) = e^{\int 3x^2 \ dx}\), lo que es igual a \(e^{x^3}\).

Luego multiplicamos ambos lados de la ecuación por el recién calculado factor de integración.

$$e^{x^3}\frac{dy}{dx} + 3x^2e^{x^3}y = 6x^2e^{x^3}$$

simplificando, obtenemos:

$$\frac{d}{dx}(e^{x^3}y) = 6x^2e^{x^3}$$

Por último, integramos ambos lados de la ecuación:

$$e^{x^3}y = \int 6x^2e^{x^3} \ dx = 2e^{x^3} + C$$

y podemos obtener la solución final:

$$y = Ce^{-x^3} +2 $$

Condición inicial

Cuando utilizamos Ecuaciones diferenciales, generalmente no estamos interesados en encontrar una familia de soluciones (la solución general), como la que hayamos en el caso precedente, sino que vamos a estar más interesados en una solución que satisface un requerimiento particular.En muchos problemas físicos debemos de encontrar una solución particular que satisface una condición de la forma \(y(t_o) = y_0\). Esto se conoce como la condición inicial, y el problema de encontrar una solución de la Ecuación diferencial que satisface la condición inicial se conoce como el problema de valor inicial.

Series de potencias

Cuando comenzamos a lidiar con las Ecuaciones diferenciales, veremos que existen un gran número de ellas que no pueden ser resueltas en forma analítica utilizando los principios del Cálculo integral y el Cálculo diferencial; pero sin embargo, tal vez podamos encontrar soluciones aproximadas para este tipo de ecuaciones en términos de Series de potencias.

¿Qué es una serie de potencias?

Una Serie de potencias es una serie, generalmente infinita, que posee la siguiente forma:

$$\sum_{n=0}^{\infty} C_nX^n = C_0 + C_1X + C_2X^2 + C_3X^3 + \dots $$

En dónde \(x\) es una variable y las \(C_n\) son constantes o los coeficientes de la serie. Una Serie de potencias puede converger para algunos valores de \(x\) y divergir para otros valores de \(x\). La suma de la serie es una función.

$$\begin{array} f(x) = C_0 + C_1X + C_2X^2 + \\ C_3X^3 + \dots + C_nX^n + \dots \end{array} $$

El dominio de esta función va a estar dado por el conjunto de todos los \(x\) para los que la serie converge.

Series de Taylor

Las Series de Taylor son un caso especial de Serie de potencias cuyos términos adoptan la forma \((x - a)^n\). Las Series de Taylor nos van a permitir aproximar funciones continuas que no pueden resolverse en forma analítica y se van a calcular a partir de las derivadas de estas funciones. Su definición matemática es la siguiente:

$$f(x) = \sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x - a)^n$$

Lo que es equivalente a decir:

$$\begin{array} f(x) = f(a) + \frac{f'(a)}{1!}(x -a) + \frac{f''(a)}{2!}(x -a)^2 + \\ \frac{f'''(a)}{3!}(x -a)^3 + \dots \end{array} $$

Una de las razones de que las Series de Taylor sean importantes es que nos permiten integrar funciones que de otra forma no podíamos manejar. De hecho, a menudo Newton integraba funciones por medio de, en primer lugar, expresarlas como Series de potencias y luego integrando la serie término a término. Por ejemplo, la función \(f(x) = e^{-x^2}\), no puede ser integrada por los métodos normales del Cálculo integral, por lo que debemos recurrir a las Series de Taylor para aproximar la solución de su integral. Podríamos construir la Serie de Taylor de esta función, del siguiente modo:

$$\begin{array} e^{-x^2} = \sum_{n=0}^{\infty}\frac{(-x^2)^n}{n!} = \sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{n!} = \\ 1 - \frac{x^2}{1!} + \frac{x^4}{2!} -\frac{x^6}{3!} + \dots \end{array} $$

Resolviendo Ecuaciones diferenciales con Python

Mientras que algunos problemas de Ecuaciones diferenciales ordinarias se pueden resolver con métodos analíticos, como hemos mencionado anteriormente, son mucho más comunes los problemas que no se pueden resolver analíticamente. Por lo tanto, en estos casos debemos recurrir a los métodos numéricos. Es aquí, dónde el poder de las computadoras y en especial, de los paquetes científicos de Python como NumPy, Matplotlib, SymPy y SciPy, se vuelven sumamente útiles. Veamos como podemos utilizar la fuerza computacional para resolver Ecuaciones diferenciales.

Soluciones analíticas con Python

SymPy nos proporciona un solucionador genérico de Ecuaciones diferenciales ordinarias, sympy.dsolve, el cual es capaz de encontrar soluciones analíticas a muchas EDOs elementales. Mientras sympy.dsolve se puede utilizar para resolver muchas EDOs sencillas simbólicamente, como veremos a continuación, debemos tener en cuenta que la mayoría de las EDOs no se pueden resolver analíticamente. Por ejemplo, retomando el ejemplo que resolvimos analíticamente más arriba, veamos si llegamos al mismo resultado utilizando SymPy para solucionar la siguiente Ecuación diferencial ordinaria:

$$\frac{dy}{dx} = -3x^2y + 6x^2$$
Ver Código 
# <!-- collapse=True -->
# importando modulos necesarios
%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
import sympy 
from scipy import integrate

# imprimir con notación matemática.
sympy.init_printing(use_latex='mathjax') 

# Resolviendo ecuación diferencial
# defino las incognitas
x = sympy.Symbol('x')
y = sympy.Function('y')

# expreso la ecuacion
f = 6*x**2 - 3*x**2*(y(x))
sympy.Eq(y(x).diff(x), f)
$$\frac{d}{d x} y{\left (x \right )} = - 3 x^{2} y{\left (x \right )} + 6 x^{2}$$

Aquí primero definimos la incógnitas \(x\) utilizando el objeto Symbol e \(y\), que al ser una función, la definimos con el objeto Function, luego expresamos en Python la ecuación que define a la función. Ahora solo nos restaría aplicar la función dsolve para resolver nuestra EDO.

# Resolviendo la ecuación
sympy.dsolve(y(x).diff(x) - f)
$$y{\left (x \right )} = C_{1} e^{- x^{3}} + 2$$

Como podemos ver, arribamos exactamente al mismo resultado. Siguiendo el mismo procedimiento, podemos resolver otras EDOs, por ejemplo si quisiéramos resolver la siguiente Ecuación diferencial:

$$\frac{dy}{dx} = \frac{1}{2}(y^2 -1) $$

que cumpla con la condición inicial \(y(0) = 2\), debemos realizar el siguiente procedimiento:

# definiendo la ecuación
eq = 1.0/2 * (y(x)**2 - 1)

# Condición inicial
ics = {y(0): 2}

# Resolviendo la ecuación
edo_sol = sympy.dsolve(y(x).diff(x) - eq)
edo_sol
$$y{\left (x \right )} = \frac{C_{1} + e^{x}}{C_{1} - e^{x}}$$

Aquí encontramos la solución general de nuestra Ecuación diferencial, ahora reemplazamos los valores de la condición inicial en nuestra ecuación.

C_eq = sympy.Eq(edo_sol.lhs.subs(x, 0).subs(ics), edo_sol.rhs.subs(x, 0))
C_eq
$$2 = \frac{C_{1} + 1}{C_{1} - 1}$$

y por último despejamos el valor de la constante de integración resolviendo la ecuación.

sympy.solve(C_eq)
$$\left [ 3\right ]$$

Como vemos, el valor de la constante de integración es 3, por lo tanto nuestra solución para el problema del valore inicial es:

$$y{\left (x \right )} = \frac{3 + e^{x}}{3 - e^{x}}$$

Para los casos en que no exista una solución analítica, pero sí una solución aproximada por una Serie de potencias, sympy.dsolve nos va a devolver la serie como solución. Veamos el caso de la siguiente Ecuación diferencial:

$$\frac{dy}{dx} = x^2 + y^2 -1$$ 
# Solución con serie de potencias
f = y(x)**2 + x**2 -1
sympy.dsolve(y(x).diff(x) - f)
$$ \begin{array} y{\left (x \right )} = \frac{x^{3}}{3} \left(C_{1} \left(3 C_{1} - 1\right) + 1\right) + \\ \frac{x^{5}}{60} \left(C_{1} \left(4 C_{1} - 7\right) + 10 C_{1} - 6\right) + \\ C_{1} + C_{1} x + C_{1} x^{2} + \frac{C_{1} x^{4}}{12} + \mathcal{O}\left(x^{6}\right) \end{array} $$

Campos de direcciones

Los Campos de direcciones es una técnica sencilla pero útil para visualizar posibles soluciones a las ecuaciones diferenciales de primer orden. Se compone de líneas cortas que muestran la pendiente de la función incógnita en el plano x-y. Este gráfico se puede producir fácilmente debido a que la pendiente de \(y(x)\) en los puntos arbitrarios del plano x-y está dada por la definición misma de la Ecuación diferencial ordinaria:

$$\frac{dy}{dx} = f(x, y(x))$$

Es decir, que sólo tenemos que iterar sobre los valores \(x\) e \(y\) en la grilla de coordenadas de interés y evaluar \(f(x, y(x))\) para saber la pendiente de \(y(x)\) en ese punto. Cuantos más segmentos de líneas trazamos en un Campo de dirección, más clara será la imagen. La razón por la cual el gráfico de Campos de direcciones es útil, es que las curvas suaves y continuos que son tangentes a las líneas de pendiente en cada punto del gráfico, son las posibles soluciones a la Ecuación diferencial ordinaria.

Por supuesto que calcular las pendientes y dibujar los segmentos de línea para un gran número de puntos a mano sería algo realmente tedioso, pero para eso existen las computadoras y Python!. Veamos un ejemplo, supongamos que tenemos la siguiente Ecuación diferencial ordinaria, la cual según lo que vimos más arriba, sabemos que no tiene una solución analítica:

$$\frac{dy}{dx} = x^2 + y^2 -1$$

entonces, con la ayuda de Python, podemos graficar su Campo de dirección del siguiente modo:

Ver Código 
# <!-- collapse=True -->
def plot_direction_field(x, y_x, f_xy, x_lim=(-5, 5), y_lim=(-5, 5), ax=None):
    """Esta función dibuja el campo de dirección de una EDO"""
    
    f_np = sympy.lambdify((x, y_x), f_xy, modules='numpy')
    x_vec = np.linspace(x_lim[0], x_lim[1], 20)
    y_vec = np.linspace(y_lim[0], y_lim[1], 20)
    
    if ax is None:
        _, ax = plt.subplots(figsize=(4, 4))
    
    dx = x_vec[1] - x_vec[0]
    dy = y_vec[1] - y_vec[0]
    
    for m, xx in enumerate(x_vec):
        for n, yy in enumerate(y_vec):
            Dy = f_np(xx, yy) * dx
            Dx = 0.8 * dx**2 / np.sqrt(dx**2 + Dy**2)
            Dy = 0.8 * Dy*dy / np.sqrt(dx**2 + Dy**2)
            ax.plot([xx - Dx/2, xx + Dx/2],
                    [yy - Dy/2, yy + Dy/2], 'b', lw=0.5)
    
    ax.axis('tight')
    ax.set_title(r"$%s$" %
                 (sympy.latex(sympy.Eq(y(x).diff(x), f_xy))),
                 fontsize=18)
    
    return ax

# Defino incognitas
x = sympy.symbols('x')
y = sympy.Function('y')

# Defino la función
f = y(x)**2 + x**2 -1

# grafico de campo de dirección
fig, axes = plt.subplots(1, 1, figsize=(8, 6))
campo_dir = plot_direction_field(x, y(x), f, ax=axes)

png

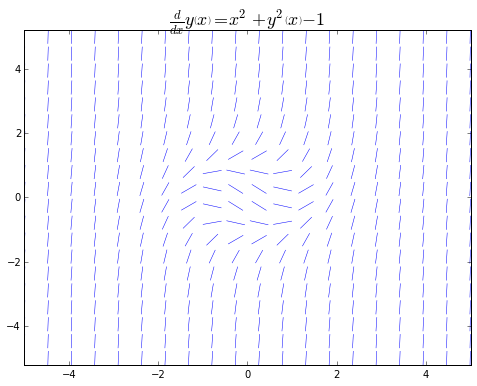
Las líneas de dirección en el gráfico de arriba sugieren cómo las curvas que son soluciones a la Ecuación diferencial ordinaria se van a comportar. Por lo tanto, los Campos de direcciones son una herramienta muy útil para visualizar posibles soluciones para Ecuaciones diferenciales ordinarias que no se pueden resolver analíticamente. Este gráfico, también nos puede ayudar a determinar el rango de validez de la solución aproximada por la Serie de potencias. Por ejemplo si resolvemos nuestra EDO para la condición inicial \(y(0) = 0\), veamos a que conclusiones arribamos.

# Condición inicial
ics = {y(0): 0}

# Resolviendo la ecuación diferencial
edo_sol = sympy.dsolve(y(x).diff(x) - f, ics=ics)
edo_sol
$$y{\left (x \right )} = - x + \frac{2 x^{3}}{3} - \frac{4 x^{5}}{15} + \mathcal{O}\left(x^{6}\right)$$ 
fig, axes = plt.subplots(1, 2, figsize=(10, 5))

# panel izquierdo - solución aproximada por Serie de potencias
plot_direction_field(x, y(x), f, ax=axes[0])
x_vec = np.linspace(-3, 3, 100)
axes[0].plot(x_vec, sympy.lambdify(x, edo_sol.rhs.removeO())(x_vec),
             'b', lw=2)

# panel derecho - Solución por método iterativo
plot_direction_field(x, y(x), f, ax=axes[1])
x_vec = np.linspace(-1, 1, 100)
axes[1].plot(x_vec, sympy.lambdify(x, edo_sol.rhs.removeO())(x_vec),
             'b', lw=2)

# Resolviendo la EDO en forma iterativa 
edo_sol_m = edo_sol_p = edo_sol
dx = 0.125

# x positivos
for x0 in np.arange(1, 2., dx):
    x_vec = np.linspace(x0, x0 + dx, 100)
    ics = {y(x0): edo_sol_p.rhs.removeO().subs(x, x0)}
    edo_sol_p = sympy.dsolve(y(x).diff(x) - f, ics=ics, n=6)
    axes[1].plot(x_vec, sympy.lambdify(x, edo_sol_p.rhs.removeO())(x_vec),
                 'r', lw=2)

# x negativos
for x0 in np.arange(1, 5, dx):
    x_vec = np.linspace(-x0-dx, -x0, 100)
    ics = {y(-x0): edo_sol_m.rhs.removeO().subs(x, -x0)}
    edo_sol_m = sympy.dsolve(y(x).diff(x) - f, ics=ics, n=6)
    axes[1].plot(x_vec, sympy.lambdify(x, edo_sol_m.rhs.removeO())(x_vec),
                 'r', lw=2)

png

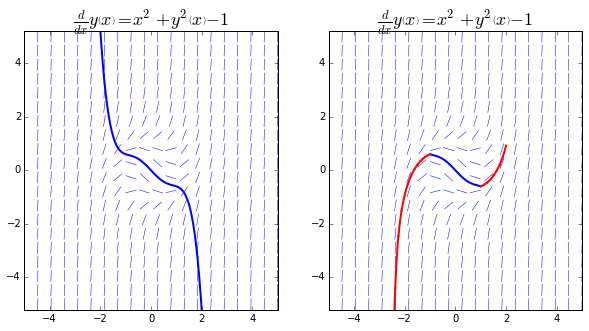
En el panel de la izquierda podemos ver el gráfico de la solución aproximada por la Serie de potencias; en el panel de la derecha vemos el gráfico al que podemos arribar resolviendo la EDO para valores incrementales de \(x\) para la condición inicial en forma iterativa. Como podemos ver, las solución aproximada se alinea bien con el campo de direcciones para los valores de \(x\) entre \(-1.5\) y \(1.5\), luego comienza a desviarse, lo que nos indica que la solución aproximada ya no sería válida. En el panel de la derecha podemos ver una solución que se adapta mucho mejor con el campo de direcciones.

Transformada de Laplace

Un método alternativo que podemos utilizar para resolver en forma analítica Ecuaciones diferenciales ordinarias complejas, es utilizar la Transformada de Laplace, que es un tipo particular de transformada integral. La idea es que podemos utilizar esta técnica para transformar nuestra Ecuación diferencial en algo más simple, resolver esta ecuación más simple y, a continuación, invertir la transformación para recuperar la solución a la Ecuación diferencial original.

¿Qué es una Transformada de Laplace?

Para poder comprender la Transformada de Laplace, primero debemos revisar la definición general de la transformada integral, la cuál adapta la siguiente forma:

$$T(f(t)) = \int_{\alpha}^{\beta} K (s, t) \ f(t) \ dt = F(s) $$

En este caso, \(f(t)\) es la función que queremos transformar, y \(F(s)\) es la función transformada. Los límites de la integración, \(\alpha\) y \(\beta\), pueden ser cualquier valor entre \(-\infty\) y \(+\infty\) y \(K(s, t)\) es lo que se conoce como el núcleo o kernel de la transformada, y podemos elegir el kernel que nos plazca. La idea es poder elegir un kernel que nos dé la oportunidad de simplificar la Ecuación diferencial con mayor facilidad.

Si nos restringimos a Ecuaciones diferenciales con coeficientes constantes, entonces un kernel que resulta realmente útil es \(e^{-st}\), ya que al diferenciar este kernel con respecto de \(t\), terminamos obteniendo potencias de \(s\), que podemos equiparar a los coeficientes constantes. De esta forma, podemos arribar a la definición de la Transformada de Laplace:

$$\mathcal{L}\{f(t)\}=\int_0^{\infty} e^{-st} \ f(t) \ dt$$

Tengan en cuenta, que además de usar el kernel \(e^{-st}\), los límites de la integración van desde \(0\) a \(\infty\), ya que valores negativos de \(t\) harían divergir la integral.

Tabla de transformadas de Laplace

Calcular la Transformada de Laplace a veces puede resultar en una tarea complicada. Por suerte, podemos recurrir a la siguiente tabla para resolver la Transformada de Laplace para las funciones más comunes:

Función original Transformada de Laplace Restricciones
$$1$$ $$\frac{1}{s}$$ $$s>0$$
$$e^{at}$$ $$\frac{1}{s -a}$$ $$s>a$$
$$t^n$$ $$\frac{n!}{s^{n+1}}$$ $$s>0$$, $$n$$ un entero $$> 0$$
$$\cos at$$ $$\frac{s}{s^2 + a^2}$$ $$s>0$$
$$\sin at$$ $$\frac{a}{s^2 + a^2}$$ $$s>0$$
$$\cosh at$$ $$\frac{s}{s^2 - a^2}$$ $$s>|a|$$
$$\sinh at$$ $$\frac{a}{s^2 - a^2}$$ $$s>|a|$$
$$e^{at}\cos bt$$ $$\frac{s- a}{(s^2 - a^2) + b^2}$$ $$s>a$$
$$e^{at}\sin bt$$ $$\frac{b}{(s^2 - a^2) + b^2}$$ $$s>a$$
$$t^n e^{at}$$ $$\frac{n!}{(s-a)^{n+1}}$$ $$s>a$$, $$n$$ un entero $$> 0$$
$$f(ct)$$ $$\frac{1}{c}\mathcal{L}\{f(s/c)\}$$ $$c>0$$

Propiedades de las transformadas de Laplace

Las Transformadas de Laplace poseen algunas propiedades que también nos van a facilitar el trabajo de resolverlas, algunas de ellas son:

$$\mathcal{L}\{c_1f_1(t) + c_2f_2(t)\}=c_1\mathcal{L}\{f_1(t)\} + c_2\mathcal{L}\{f_2(t)\}$$
  • La Transformada de Laplace de la primer derivada: Esta propiedad nos dice que si \(f(t)\) es continua y \(f’(t)\) es continua en el intervalo \(0 \le t \le \alpha\). Entonces la Transformada de Laplace de la primer derivada es:
$$\mathcal{L}\{f'(t)\} = s\mathcal{L}\{f(t)\} - f(0)$$
  • La Transformada de Laplace de derivadas de orden superior: Esta propiedad es la generalización de la propiedad anterior para derivadas de orden n. Su formula es:
$$ \begin{array} \mathcal{L}\{f^{(n)}(t)\} = s^n\mathcal{L}\{f(t)\} - s^{n-1}f(0) - \dots -f^{(n-1)}(0) \\ = s^n\mathcal{L}\{f(t)\} - \sum_{i=1}^n s^{n-i}f^{(i-1)}(0) \end{array} $$

Resolviendo ecuaciones diferenciales con la transformada de Laplace

La principal ventaja de utilizar Transformadas de Laplace es que cambia la Ecuación diferencial en una ecuación algebraica, lo que simplifica el proceso para calcular su solución. La única parte complicada es encontrar las transformaciones y las inversas de las transformaciones de los varios términos de la Ecuación diferencial que queramos resolver. Veamos entonces como Python y SymPy nos ayudan a resolver Ecuaciones diferenciales utilizando las Transformadas de Laplace. Vamos a intentar resolver la siguiente ecuación:

$$y'' + 3y' + 2y = 0$$

con las siguientes condiciones iniciales: \(y(0) = 2\) y \(y’(0) = -3\)

# Ejemplo de transformada de Laplace
# Defino las incognitas
t = sympy.symbols("t", positive=True)
y = sympy.Function("y")

# Defino la ecuación
edo = y(t).diff(t, t) + 3*y(t).diff(t) + 2*y(t)
sympy.Eq(edo)
$$2 y{\left (t \right )} + 3 \frac{d}{d t} y{\left (t \right )} + \frac{d^{2}}{d t^{2}} y{\left (t \right )} = 0$$ 
# simbolos adicionales.
s, Y = sympy.symbols("s, Y", real=True)

# Calculo la transformada de Laplace 
L_edo = sympy.laplace_transform(edo, t, s, noconds=True)
sympy.Eq(L_edo)
$$2 \mathcal{L}_{t}\left[y{\left (t \right )}\right]\left(s\right) + 3 \mathcal{L}_{t}\left[\frac{d}{d t} y{\left (t \right )}\right]\left(s\right) + \mathcal{L}_{t}\left[\frac{d^{2}}{d t^{2}} y{\left (t \right )}\right]\left(s\right) = 0$$

Como podemos ver en este resultado, al aplicar la función sympy.laplace_transform sobre la derivada de \(y(t)\), SymPy nos devuelve un termino con la forma \(\mathcal{L}_{t}\left[\frac{d}{d t} y{\left (t \right )}\right]\left(s\right)\). Esto es una complicación si queremos arribar a una ecuación algebraica. Por tanto antes de proceder, deberíamos utilizar la siguiente función para resolver este inconveniente.

def laplace_transform_derivatives(e):
    """
    Evalua las transformadas de Laplace de derivadas de funciones sin evaluar.
    """
    if isinstance(e, sympy.LaplaceTransform):
        if isinstance(e.args[0], sympy.Derivative):
            d, t, s = e.args 
            n = len(d.args) - 1
            return ((s**n) * sympy.LaplaceTransform(d.args[0], t, s) -
                    sum([s**(n-i) * sympy.diff(d.args[0], t, i-1).subs(t, 0)
                         for i in range(1, n+1)]))
        
    if isinstance(e, (sympy.Add, sympy.Mul)):
        t = type(e) 
        return t(*[laplace_transform_derivatives(arg) for arg in e.args])
    
    return e

# Aplicamos la nueva funcion para evaluar las transformadas de Laplace
# de derivadas
L_edo_2 = laplace_transform_derivatives(L_edo)
sympy.Eq(L_edo_2)
$$\begin{array} s^{2} \mathcal{L}_{t}\left[y{\left (t \right )}\right]\left(s\right) + 3 s \mathcal{L}_{t}\left[y{\left (t \right )}\right]\left(s\right) - s y{\left (0 \right )} + \\ 2 \mathcal{L}_{t}\left[y{\left (t \right )}\right]\left(s\right) - 3 y{\left (0 \right )} - \left. \frac{d}{d t} y{\left (t \right )} \right|_{\substack{ t=0 }} = 0 \end{array} $$ 
# reemplazamos la transfomada de Laplace de y(t) por la incognita Y
# para facilitar la lectura de la ecuación.
L_edo_3 = L_edo_2.subs(sympy.laplace_transform(y(t), t, s), Y)
sympy.Eq(L_edo_3)
$$Y s^{2} + 3 Y s + 2 Y - s y{\left (0 \right )} - 3 y{\left (0 \right )} - \left. \frac{d}{d t} y{\left (t \right )} \right|_{\substack{ t=0 }} = 0$$ 
# Definimos las condiciones iniciales
ics = {y(0): 2, y(t).diff(t).subs(t, 0): -3}
ics
$$\left \{ y{\left (0 \right )} : 2, \quad \left. \frac{d}{d t} y{\left (t \right )} \right|_{\substack{ t=0 }} : -3\right \}$$ 
# Aplicamos las condiciones iniciales
L_edo_4 = L_edo_3.subs(ics)
L_edo_4
$$Y s^{2} + 3 Y s + 2 Y - 2 s - 3$$ 
# Resolvemos la ecuación y arribamos a la Transformada de Laplace
# que es equivalente a nuestra ecuación diferencial
Y_sol = sympy.solve(L_edo_4, Y)
Y_sol
$$\left [ \frac{2 s + 3}{s^{2} + 3 s + 2}\right ]$$ 
# Por último, calculamos al inversa de la Transformada de Laplace que 
# obtuvimos arriba, para obtener la solución de nuestra ecuación diferencial.
y_sol = sympy.inverse_laplace_transform(Y_sol[0], s, t)
y_sol
$$\frac{e^{t} + 1}{e^{2 t}}$$ 
# Comprobamos la solución.
y_sol.subs(t, 0), sympy.diff(y_sol).subs(t, 0)
$$\left ( 2, \quad -3\right )$$

Como podemos ver Transformadas de Laplace, pueden ser una buena alternativa para resolver Ecuaciones diferenciales en forma analítica. Pero aún así, siguen existiendo ecuaciones que se resisten a ser resueltas por medios analíticos, para estos casos, debemos recurrir a los métodos numéricos.

Métodos numéricos

Cuando todo lo demás falla, llegan los métodos numéricos al rescate; siempre vamos a poder calcular una aproximación numérica a una solución de una Ecuación diferencial. De éstos métodos ya no vamos a obtener las formulas elegantes y acabadas que veníamos viendo, sino que vamos a obtener números. Existen muchos enfoques para resolver ecuaciones diferenciales ordinarias en forma numérica, y generalmente están diseñados para resolver problemas que están formulados como un sistema de ecuaciones diferenciales de primer orden de la forma estándar:

$$ \frac{dy}{dx} = f(x, y(x))$$

donde \(y(x)\) es un vector de la funciones incógnitas de \(x\).

La idea básica de muchos de los métodos numéricos para resolver ecuaciones diferenciales ordinarias es capturada por el Método de Euler, veamos de que se trata este método.

El Método de Euler

Para entender este método, revisemos nuevamente la siguiente Ecuación diferencial:

$$ \frac{dy}{dx} = f(x, y(x))$$

El Método de Euler señala que puede que no tengamos la función real que representa la solución a la Ecuación diferencial precedente. Sin embargo, si poseemos la pendiente de la curva en cualquier punto. Es decir, el ritmo de cambio de la curva, que no es otra cosa que su derivada, la cual podemos utilizar para iterar sobre soluciones en distintos puntos.

Supongamos entonces que tenemos el punto \((x_0, y_0)\), que se encuentra en la curva solución. Dada la definición de la ecuación que estamos analizando, sabemos que la pendiente de la curva solución en ese punto es \(f(x_0, y_0)\). ¿Qué pasaría entonces si quisiéramos encontrar la solución numérica en el punto \((x, y)\) que se encuentra a una corta distancia \(h\)?. En este caso, podríamos definir a \(y\) como \(y = y_0 + \Delta y\), es decir, \(y\) va ser igual al valor de \(y\) en el punto inicial, más el cambio que ocurrió en \(y\) al movernos a la distancia \(h\). Y como el cambio en \(y\) va a estar dado por la pendiente de la curva, que en este caso sabemos que es igual a \(f(x_0, y_0)\), podemos definir la siguiente relación de recurrencia que es la base para encontrar las soluciones numéricas con el Método de Euler:

$$y = y_0 + f(x_0, y_0)h$$

La cual podemos generalizar para todo \(n\) del siguiente forma:

$$y_n = y_{n -1} + f(x_{n - 1}, y_{n - 1})h$$

.

Este método esta íntimamente relacionado con los Campos de direcciones que analizamos más arriba. En general, el Método de Euler dice que empecemos por el punto dado por el condición incial y continuemos en la dirección indicada por el Campo de direcciones. Luego nos detengamos, miramos a la pendiente en la nueva ubicación, y procedemos en esa dirección.

El Método de Runge-Kutta

Otro método que podemos utilizar para encontrar soluciones numéricas a Ecuaciones diferenciales, y que incluso es más preciso que el Método de Euler, es el Método de Runge-Kutta. En el cual la relación de recurrencia va a estar dada por un promedio ponderado de términos de la siguiente manera:

$$y_{k + 1} = y_k + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)$$

en dónde:

$$ \begin{array} k_1 = f(x_k, y_k)h_k, \\ k_2 = f\left(x_k + \frac{h_k}{2}, y_k + \frac{k_1}{2}\right)h_k, \\ k_3 = f\left(x_k + \frac{h_k}{2}, y_k + \frac{k_2}{2}\right)h_k, \\ k_4 = f\left(x_k + h_k, y_k + k_3\right)h_k. \\ \end{array} $$

Soluciones numéricas con Python

Para poder resolver Ecuaciones diferenciales en forma numérica con Python, podemos utilizar las herramienta de integración que nos ofrece SciPy, particularmente los dos solucionadores de ecuaciones diferenciales ordinarias, integrate.odeint y integrate.ode. La principal diferencia entre ambos, es que integrate.ode es más flexible, ya que nos ofrece la posibilidad de elegir entre distintos solucionadores. Veamos algunos ejemplos:

Comencemos por la siguiente función:

$$f(x, y(x)) = x + y(x)^2$$ 
# Defino la función
f = y(x)**2 + x
f
$$x + y^{2}{\left (x \right )}$$ 
# la convierto en una función ejecutable
f_np = sympy.lambdify((y(x), x), f)

# Definimos los valores de la condición inicial y el rango de x sobre los 
# que vamos a iterar para calcular y(x)
y0 = 0
xp = np.linspace(0, 1.9, 100)

# Calculando la solución numerica para los valores de y0 y xp
yp = integrate.odeint(f_np, y0, xp)

# Aplicamos el mismo procedimiento para valores de x negativos
xn = np.linspace(0, -5, 100)
yn = integrate.odeint(f_np, y0, xn)

Los resultados son dos matrices unidimensionales de NumPy \(yp\) y \(yn\), de la misma longitud que las correspondientes matrices de coordenadas \(xp\) y \(xn\), que contienen las soluciones numéricas de la ecuación diferencial ordinaria para esos puntos específicos. Para visualizar la solución, podemos graficar las matrices \(yp\) y \(yn\), junto con su Campo de direcciones.

fig, axes = plt.subplots(1, 1, figsize=(8, 6))
plot_direction_field(x, y(x), f, ax=axes)
axes.plot(xn, yn, 'b', lw=2)
axes.plot(xp, yp, 'r', lw=2)
plt.show()

png

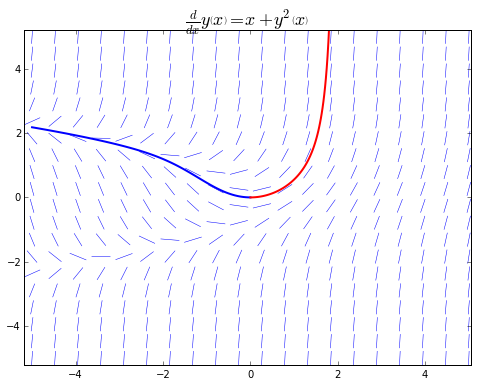
En este ejemplo, solucionamos solo una ecuación. Generalmente, la mayoría de los problemas se presentan en la forma de sistemas de ecuaciones diferenciales ordinarias, es decir, que incluyen varias ecuaciones a resolver. Para ver como podemos utilizar a integrate.odeint para resolver este tipo de problemas, consideremos el siguiente sistema de ecuaciones diferenciales ordinarias, conocido el atractor de Lorenz:

$$x'(t) = \sigma(y -x), \\ y'(t) = x(\rho -z)-y, \\ z'(t) = xy - \beta z $$

Estas ecuaciones son conocidas por sus soluciones caóticas, que dependen sensiblemente de los valores de los parámetros \(\sigma\), \(\rho\) y \(\beta\). Veamos como podemos resolverlas con la ayuda de Python.

# Definimos el sistema de ecuaciones
def f(xyz, t, sigma, rho, beta):
    x, y, z = xyz
    return [sigma * (y - x), 
           x * (rho - z) - y,
           x * y - beta * z]

# Asignamos valores a los parámetros
sigma, rho, beta = 8, 28, 8/3.0

# Condición inicial y valores de t sobre los que calcular
xyz0 = [1.0, 1.0, 1.0]
t = np.linspace(0, 25, 10000)

# Resolvemos las ecuaciones
xyz1 = integrate.odeint(f, xyz0, t, args=(sigma, rho, beta))
xyz2 = integrate.odeint(f, xyz0, t, args=(sigma, rho, 0.6*beta))
xyz3 = integrate.odeint(f, xyz0, t, args=(2*sigma, rho, 0.6*beta))

# Graficamos las soluciones
from mpl_toolkits.mplot3d.axes3d import Axes3D
fig, (ax1,ax2,ax3) = plt.subplots(1, 3, figsize=(12, 4),
                                  subplot_kw={'projection':'3d'})

for ax, xyz, c in [(ax1, xyz1, 'r'), (ax2, xyz2, 'b'), (ax3, xyz3, 'g')]:
    ax.plot(xyz[:,0], xyz[:,1], xyz[:,2], c, alpha=0.5)
    ax.set_xlabel('$x$', fontsize=16)
    ax.set_ylabel('$y$', fontsize=16)
    ax.set_zlabel('$z$', fontsize=16)
    ax.set_xticks([-15, 0, 15])
    ax.set_yticks([-20, 0, 20])
    ax.set_zticks([0, 20, 40])

png

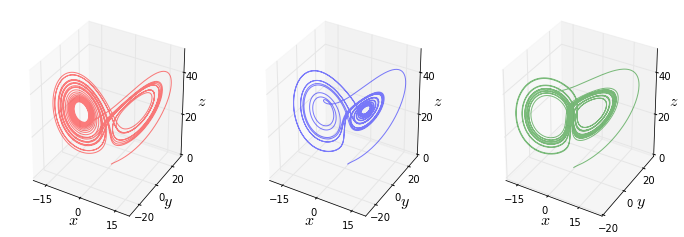
Como podemos ver, los solucionadores numéricos que nos ofrece SciPy son simples de utilizar y pueden simplificar bastante el trabajo de resolver Ecuaciones diferenciales.

Método analítico vs Método numérico

Al resolver una ecuación diferencial ordinaria en forma analítica, el resultado es una función, \(f\), que nos permite calcular la población, \(f(t)\), para cualquier valor de \(t\). Al resolver una ecuación diferencial ordinaria en forma numéricamente, se obtienen dos matrices de una dimensión. Podemos pensar a estas matrices como una aproximación discreta de la función continua \(f\): “discreta”, ya que sólo se define para ciertos valores de \(t\), y “aproximada”, porque cada valor \(F_i\) es sólo una estimación del verdadero valor de \(f(t)\). Por tanto, estas son limitaciones de las soluciones numéricas. La principal ventaja es que se puede calcular soluciones numéricas de ecuaciones diferenciales ordinarias que no tienen soluciones analíticas, que son la gran mayoría de las ecuaciones diferenciales ordinarias no lineales.

Con esto concluyo este paseo por una de las más fructíferas ideas de las matemáticas aplicadas, las Ecuaciones diferenciales; espero que les pueda servir de guía para facilitarles su solución.

Saludos!

Este post fue escrito utilizando Jupyter notebook. Pueden descargar este notebook o ver su version estática en nbviewer.