"Sólo hay 10 tipos de personas en el mundo: Los que entienden binario y los que no lo hacen."

Introducción¶

El sistema de números binarios es el más fundamental sistema numérico que se utiliza en todas las computadoras. Cualquier dispositivo digital que vemos hoy en día, desde celulares hasta Smart TVs utilizan el sistema binario! Este sistema sigue reglas muy similares al sistema decimal (el que usamos diariamente) pero en lugar de utilizar una base decimal de 10 números, se utiliza una base de 2 números, cero y uno. Es decir que los números van a ser expresados como una cadena de 1s y 0s.

Una de las formas más sencillas de entender este sistema de numeración, es comparándolo con algo que ya conocemos y que manejamos cotidianamente como es el sistema decimal. Comencemos viendo como convertir los números entre estos dos sistemas.

Convertir un número Binario a Decimal¶

Como en cualquier sistema de numeración, en los números binarios cada dígito tiene distinto valor dependiendo de la posición en que se encuentre dentro de la cadena. Para convertir un número binario en su equivalente en decimal, solamente debemos conocer las potencias de 2 y luego es cuestión de contar las posiciones. Algo a tener en cuenta es que al trabajar con binarios los algoritmos en general se aplican de derecha a izquierda. Entonces, vamos a empezar a contar desde la derecha y a cada posición le vamos a asignar una potencia de 2 empezando por el 0. Por ejemplo, si queremos convertir el 10011000 al sistema decimal, deberíamos hacer lo siguiente:

Le asignamos las potencias a cada posición y luego multiplicamos los resultados de las potencias por los 1 y 0; por último sumamos los resultados y obtenemos la conversión en el sistema decimal 128 + 16 + 8 = 152.

Convertir un número Decimal a Binario¶

Realizar el proceso inverso y convertir un número decimal a un número binario también es bastante sencillo. Como el sistema binario solo tiene 2 alternativas 0 y 1; el número 2 se vuelve fundamental. Para convertir un número decimal a su equivalente en binario entonces tenemos que comenzar a dividir por 2 hasta obtener restos de 1 y 0. Por ejemplo si queremos convertir el número 152, debemos ir dividiendo el mismo por 2 como podemos ver en el siguiente cuadro:

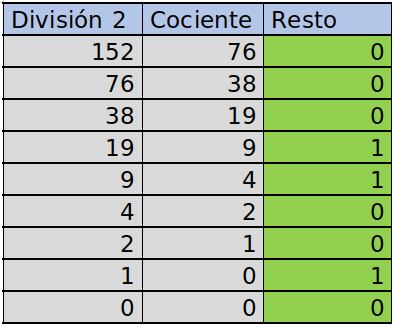
Una vez que completamos este proceso, simplemente tomamos los restos desde abajo hacia arriba y obtenemos el número binario equivalente, que en este caso es 10011000.

Suma de números Binarios¶

La suma de números binarios es bastante fácil, solo hay que tener en cuenta la siguiente tabla y luego es un proceso simple y mecánico:

Es decir 0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1 y 1 + 1 = 10. En este último caso en realidad el resultado de 1 + 1 es 0 y se arrastra un 1 a la izquierda.

Por ejemplo, para sumar los siguientes números: 10011000 (que representa al número 152 en el sistema decimal) y 10101 (que representa al número 21), deberíamos aplicar las reglas del cuadro de la siguiente forma:  

El proceso siempre se empieza de la derecha hacia la izquierda. Tener en cuenta que en la tercera posición, el resultado de 0 + 0 es 1 porque se arrastró el valor de la suma anterior de 1 + 1 = 0. El resultado final que obtuvimos fue 10101101 el cual representa al 173 en el sistema decimal!.

Resta de números Binarios¶

Para la resta de números binarios el algoritmo es también muy fácil y similar al que se utiliza en el sistema decimal. El cuadro a tener en cuenta en este caso es:

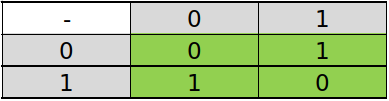
Es decir 0 - 0 = 0; 1 - 0 = 1; 1 - 1 = 0 y 0 - 1 = 1. En este último caso en realidad como no se puede restar 1 a 0, se pide prestado una unidad de la posición siguiente como hacemos en la resta en el sistema decimal.

Por ejemplo, para restar los siguientes números: 11001001 (que representa al 201 en decimales) y 1000011 (que representa al 67), deberíamos aplicar las reglas del cuadro de la siguiente forma:

Nuevamente el algoritmo se aplica de derecha a izquierda, comenzamos con 1 – 1 que da 0, luego 0 – 1 que da 1 y arrastramos a 1 a la izquierda, por lo que la siguiente columna vuelve a ser 0 – 1 que da 1, como volvimos a arrastrar la siguiente es 1 – 1 igual a 0 y después ya es más simple porque ya no tenemos arrastres. El resultado final es 10000110 que representa al número 134 en el sistema decimal!

Multiplicación de números Binarios¶

El algoritmo de multiplicación es similar al que utilizamos en el sistema decimal pero es mucho más sencillo ya que solo tenemos que multiplicar por 1 y 0! La tabla que utilizamos para los cálculos es la siguiente:

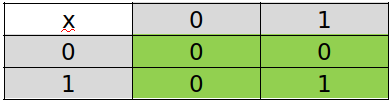
Para poder realizar la multiplicación al igual que como ocurre con el sistema decimal, tenemos que saber sumar. Por ejemplo, si queremos multiplicar 10110 (22 en el sistema decimal) por 1001 ( que representa al 9) el proceso sería el siguiente:

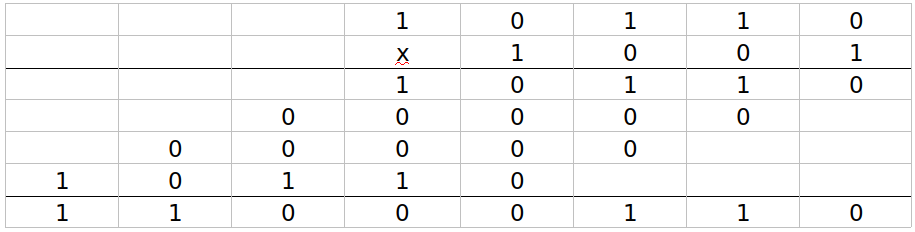
Vamos multiplicando dígito a dígito y luego sumamos los resultados; el resultado final es 11000110 que equivale a 198 en el sistema decimal.

División de números Binarios¶

El algoritmo de división de números binarios es el mismo que se utiliza para el sistema decimal con la salvedad que solo podemos trabajar con 1s y 0s y que las restas y multiplicaciones se deben realizar también en binario.

Si por ejemplo queremos dividir 101010 (que representa al 42 en el sistema decimal) entre 110 (que representa al 6); el proceso sería el siguiente:

Tomamos los primeros 3 dígitos 101 como 101 (5 en decimal) es más chico que 110 (6 en decimal) no nos sirve, entonces tomamos un dígito más 1010. Como es más grande entonces entra 1 vez en 110, por lo que ya tenemos el primer dígito del resultado. Multiplicamos 1 por 110 y lo restamos a 1010, el resultado es 100, como 100 es menor que 110 bajamos el siguiente dígito, por lo que nos queda 1001 para dividir entre 110.

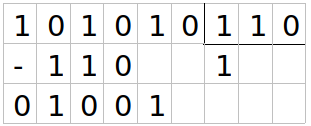
Como 1001 es mayor que 110, volvemos a aplicar el procedimiento y restar 110.

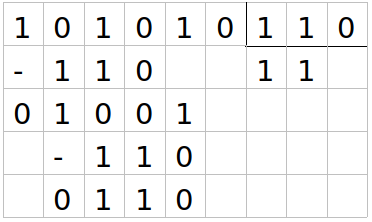
Como 110 entra una vez en 110, otra vez obtenemos 1 y volvemos a aplicar el procedimiento.

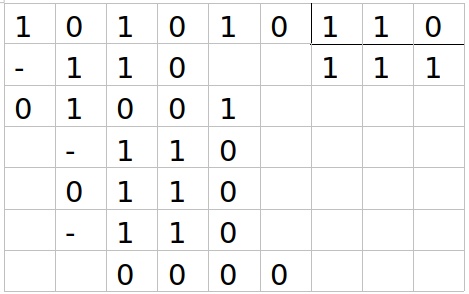
De esta forma arribamos al resultado final de 111 ( 7 en el sistema decimal).

Como la división es un poco más difícil que las otras operaciones, realicemos un ejemplo más, en este caso vamos a dividir 101000 (40 en decimal) entre 1000 (8 en decimal).

Partimos de los primeros 4 dígitos, como 1010 es mayor que 1000, el primer dígito de nuestro resultado es 1.

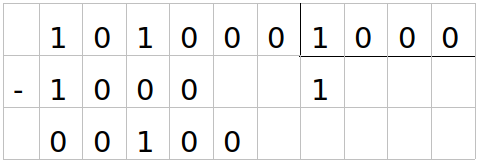
Luego de restar 1000 a 1010, el resultado es 10, como es más chico que 1000 bajamos el siguiente dígito; como 100 sigue siendo más chico que 1000; el segundo dígito de nuestro resultado es 0.

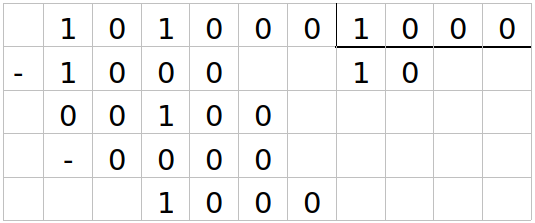
Continuamos aplicando el mismo procedimiento; como luego de la resta, 100 sigue siendo más chico que 1000, bajamos el siguiente dígito. Ahora como 1000 entra una vez en 1000, podemos obtener el siguiente dígito del resultado y arribar al resultado final!

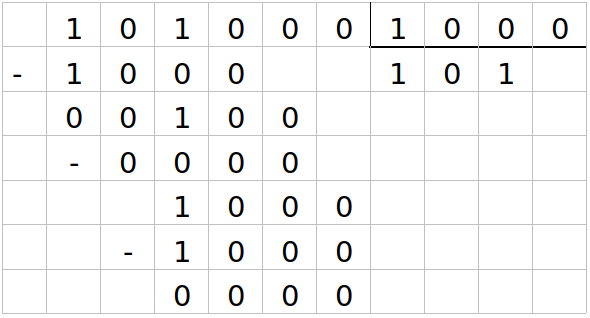
Como vemos, el resultado final es 101 que equivale a 5 en el sistema decimal.

Números Binarios con Python¶

Ahora que ya conocemos como trabajar con el sistema de números binarios en forma manual; podemos simplificar las cosas ayudándonos de Python y su interprete interactivo. En Python podemos convertir un número decimal en su equivalente en binario utilizando la función bin()

Como vemos, las operaciones entre los sistema de numeración son equivalentes, ya que lo que cambia es la forma en que representamos los números y no la esencia de la operación.

Aquí concluye este artículo, como podemos ver el sistema de numeración binario posee una simpleza muy bella que lo hace extremadamente útil; con tan solo dos estados...uno y cero, podemos representar cosas extremadamente complejas como son todos los productos de la revolución digital que utilizamos hoy en día!

Este post fue escrito por Raúl e. López Briega utilizando Jupyter notebook. Pueden descargar este notebook o ver su version estática en nbviewer.