Fractales con Python

Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Matemáticas, Analisis de datos y Python. El contenido esta bajo la licencia BSD.

“El científico no estudia la naturaleza por la utilidad que le pueda reportar; la estudia por el gozo que le proporciona, y este gozo se debe a la belleza que hay en ella…”

Henri Poincaré

“Ni las nubes son esféricas, ni las montañas cónicas, ni las costas circulares, ni el tronco de un árbol cilíndrico, ni un rayo viajan en línea recta…”

Benoît Mandelbrot

Introducción#

Para muchas personas, la palabra Geometría evoca círculos, cuadrados, cubos y otros objetos regulares o lisos. En nuestra vida cotiana, vemos edificios, muebles o automóviles, que hacen un uso amplio de tales formas. Sin embargo, muchos fenómenos en la naturaleza y la ciencia son cualquier cosa menos regulares o suaves. Por ejemplo, un paisaje natural puede incluir arbustos, árboles, montañas y nubes, que son demasiado complejas para ser representadas por las formas geométricas clásicas.

Sorprendentemente, los objetos aparentemente complejos e irregulares a menudo se pueden describir en términos notablemente simples. La Geometría fractal proporciona un marco en el que un proceso simple, que implica una operación básica repetida muchas veces, puede dar lugar a un resultado altamente irregular. Las construcciones fractales pueden representar objetos naturales pero también dan lugar a una gran variedad de otras formas, que pueden ser de extraordinaria complejidad. A menudo se escucha la frase “la belleza de los fractales”, una frase que refleja la complejidad interminable de los diseños fractales junto con la simplicidad que subyace en su forma siempre repetida.

El padre de los Fractales#

Benoît Mandelbrot, un científico colorido y poco convencional, un matemático polaco nacionalizado francés y estadounidense; es generalmente referido como el “padre de los fractales” . En su libro de 1982 “La geometría fractal de la naturaleza”, argumentó que los objetos muy irregulares deben considerarse como algo muy común, en lugar de excepcional; y además, muchos fenómenos de la Física, la Biología, las Finanzas y las Matemáticas tienen irregularidades de siguen un patrón similar. Mandelbrot introdujo la palabra fractal como una descripción general de una gran clase de objetos irregulares, y destacó la necesidad de desarrollar una matemática fractal, o en algunos casos recuperarla de documentos olvidados.

Desde la década de 1980, los fractales han atraído un interés generalizado. Prácticamente todas las áreas de la ciencia han sido examinadas desde un punto de vista fractal, con la Geometría fractal convirtiéndose en un área importante de las Matemáticas, tanto como un tema de interés por derecho propio y como una herramienta para una amplia gama de aplicaciones.

Construyendo Fractales - La curva de Koch#

Para apreciar la belleza de los fractales comencemos construyendo uno de ellos. Imaginemos una línea recta y dividámosla en tres partes iguales; luego borramos la pieza del medio y la reemplazamos por otros dos lados de un triángulo equilátero (es decir, de lados iguales) en la misma base. Esto nos dará una cadena de cuatro segmentos más cortos, unidos y en línea recta como la siguiente figura:

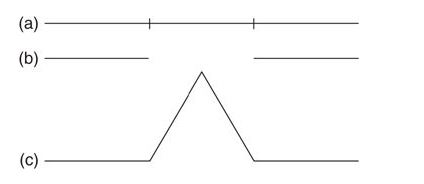
Ahora hagamos exactamente lo mismo con cada una de estas cuatro piezas: quitamos los tercios medios y los reemplazamos por los otros dos lados de los triángulos equiláteros en la misma base, para obtener una nueva cadena de 16 piezas rectas. De esta forma, podemos continuar repitiendo este proceso una y otra vez.

Ayudémosnos de Python para ver como crece en complejidad y hermosura esta figura al repitir un proceso tan simple una y otra vez.

# <!-- collapse=True -->
# Importando las librerías que vamos a utilizar
from fractal import Sierpinski, Vicsek, Tree, Dragon, Koch, Hilbert, Levy

koch = Koch()
koch.plot()

Esta figura que acabamos de construir es conocida como Curva de Koch, y fue introducida y estudiada por el matemático sueco Helge von Koch.

Propiedades de los Fractales#

Analizando esta construcción, podemos resumir las principales propiedades que exiben la mayoría de los fractales

• Estructura fina: Al ampliar la curva, por mucho que la amplifiquemos, las irregularidades en su forma siempre son evidentes. Esta es una consecuencia directa de la construcción en la que los segmentos de línea muy pequeños se trataron de la misma manera que el original pero en una escala mucho menor.

• Auto-similitud: La curva está compuesta de pequeñas copias de sí misma.

• Los métodos clásicos de geometría y matemáticas no son aplicables: La figura es demasiado irregular para ser descrito en el lenguaje geométrico tradicional y, a diferencia de las formas clásicas, no puede expresarse mediante una fórmula “simple”.

• El “Tamaño” depende de la escala a la que se mide: A diferencia de figuras tradicionales como el círculo, dónde podemos tratar de medir la longitud tomando pequeños tramos y multiplicando por el número de pasos; tratar de medir la longitud de la curva de Koch dividiéndola en pasos cada vez más cortos solo proporciona estimaciones cada vez mayores para su longitud.

• Una construcción recursiva simple: Si bien la curva parace un objeto complejo, en realidad se trata de una construcción recursiva que consiste en aplicar unos pasos simples una y otra vez.

• Una apariencia natural: Con un poco de imaginación, la mayoría de los objetos fractales toman formas que recuerdan a la Naturaleza.

Otros Ejemplos de Fractales#

Algunos otros ejemplos de fractales son:

La curva de Levy C#

Esta curva lleva el nombre por el matemático francés Paul Pierre Lévy quien, en 1938, fue el primero en exhibir sus propiedades de autosimilaridad y proveer una construcción geométrica.

levy = Levy()
levy.plot()

La curva de Hilber#

Este fractal, descripto por David Hilbert es una variante de las curvas de Peanno que recubren todo el plano.

hilbert = Hilbert()
hilbert.plot()

La curva del Dargon#

Este fractal hizo su aparición por primera vez en la columna de juegos matematicos de Martín Gardner en Scientific American.

dragon = Dragon()
dragon.plot()

El triangulo de Sierpinski#

Propuesto por el matemático polaco Wacław Sierpiński. Este fractal se puede construir a partir de cualquier triángulo.

sierpinski = Sierpinski()
sierpinski.plot()

El Fractal de Vicsek#

Es un fractal propuesto por Tamás Vicsek. Es utilizado en el diseño de antenas compactas, particularmente para teléfonos celulares.

vicsek = Vicsek()
vicsek.plot()

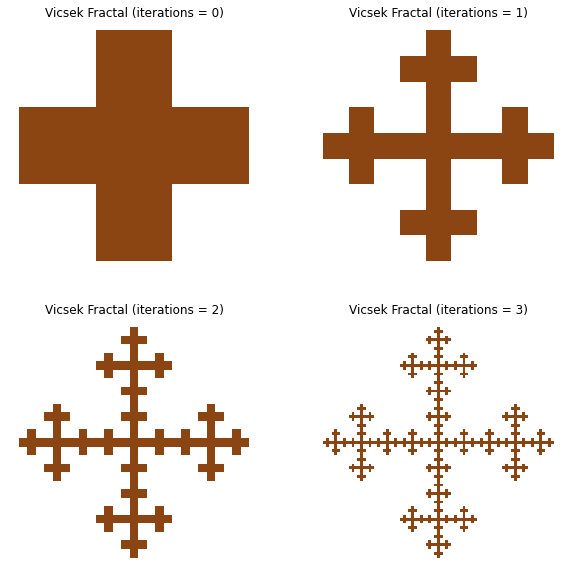
Fractales en el mundo real#

Los fractales que vimos hasta aquí viven en el mundo idealizado de las Matemáticas, donde es teóricamente posible repetir cada paso de construcción en forma indefinida, o ver un objeto a escalas arbitrariamente pequeñas. Por supuesto, el “mundo real” no es así, en la realidad, solo encontramos fractales aproximados. Si nos acercamos demasiado a un objeto real, se perderá cualquier auto-similitud, y eventualmente nos encontraremos con una estructura molecular o atómica. Sin embargo, puede ser muy útil considerar los objetos naturales como fractales si exhiben irregularidades o auto-similitudes cuando se ven en un rango significativo de escalas.

Algunos casos de fractales que podemos encontrar en la Madre Naturaleza son:

• Costas y paisajes: Las formas geográficas, como las costas, los paisajes y los causes de los ríos muestran muchas características fractales.

• Nubes: La forma de las nubes es complicada e irragular, tomando muchas de las características de los fractales.

• El brócoli romanesco: Su estructura general está compuesta por una serie de conos repetidos a escalas cada vez más pequeñas.

• Ramas de los árboles: Las ramas de los árboles crecen y se bifurcan siguiendo un patrón de autosimilitud como el de los fractales.

tree = Tree()
tree.plot()

Aquí concluye este fascinante paseo por el mundo de los fractales. Espero que hayan disfrutado del artículo.

Saludos!

Este post fue escrito por Raúl e. López Briega utilizando Jupyter notebook. Pueden descargar este notebook o ver su version estática en nbviewer.