Más Álgebra lineal con Python

Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Matemáticas, análisis de datos y python. El contenido esta bajo la licencia BSD.

Introducción#

El Álgebra lineal constituye la base de gran parte de las matemáticas modernas, ya sea en su fase teórica, aplicada, o computacional. Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas, como ser: el análisis funcional, las ecuaciones diferenciales, la investigación operativa, la econometría y la ingeniería. Es por esto, que se vuelve sumamente importante conocer sus métodos en profundidad.

La idea de este artículo, es profundizar alguno de los temas que ya vimos en mi artículo anterior (Álgebra lineal con Python), presentar algunos nuevos, e ilustrar la utilidad de esta rama de la matemáticas con alguna de sus aplicaciones.

Campos#

Un Campo, $F$, es una estructura algebraica en la cual las operaciones de adición y multiplicación se pueden realizar y cumplen con las siguientes propiedades:

1. La propiedad conmutativa tanto para la adición como para la multiplicación; es decir: $a+b=b+a$; y $a\cdot b=b\cdot a$; para todo $a,b\in F$

2. La propiedad asociativa, tanto para la adición como para la multiplicación; es decir: $(a+b)+c=a+(b+c)$; y $(a\cdot b)\cdot c=a\cdot (b\cdot c)$; para todo $a,b,c\in F$

3. La propiedad distributiva de la multiplicación sobre la adición; es decir: $a\cdot (b+c)=a\cdot b+a\cdot c$; para todo $a,b,c\in F$

4. La existencia de un elemento neutro tanto para la adición como para la multiplicación; es decir: $a+0=a$; y $a\cdot 1=a$; para todo $a\in F$.

5. La existencia de un elemento inverso tanto para la adición como para la multiplicación; es decir: $a+(-a)=0$; y $a\cdot a^{-1}=1$; para todo $a\in F$ y $a\ne 0$.

Dos de los Campos más comunes con los que nos vamos a encontrar al trabajar en problemas de Álgebra lineal, van a ser el conjunto de los números reales, $\mathbb{R}$; y el conjunto de los números complejos, $\mathbb{C}$.

Vectores#

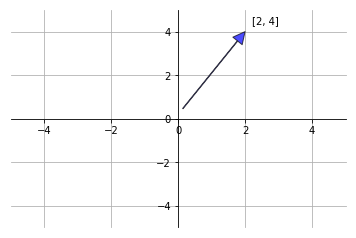
Muchas nociones físicas, tales como las fuerzas, velocidades y aceleraciones, involucran una magnitud (el valor de la fuerza, velocidad o aceleración) y una dirección. Cualquier entidad que involucre magnitud y dirección se llama vector. Los vectores se representan por flechas en las que la longitud de ellas define la magnitud; y la dirección de la flecha representa la dirección del vector. Podemos pensar en los vectores como una serie de números. Éstos números tienen una orden preestablecido, y podemos identificar cada número individual por su índice en ese orden. Los vectores identifican puntos en el espacio, en donde cada elemento representa una coordenada del eje en el espacio. La típica forma de representarlos es la siguiente:

Geométricamente podemos representarlos del siguiente modo en el plano de 2 dimensiones:

# <!-- collapse=True -->
# importando modulos necesarios
%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
import scipy.sparse as sp
import scipy.sparse.linalg
import scipy.linalg as la
import sympy

# imprimir con notación matemática.
sympy.init_printing(use_latex='mathjax')

# <!-- collapse=True -->
# graficando vector en R^2 [2, 4]
def move_spines():
    """Crea la figura de pyplot y los ejes. Mueve las lineas de la izquierda
    y de abajo para que se intersecten con el origen. Elimina las lineas de
    la derecha y la de arriba. Devuelve los ejes."""
    fix, ax = plt.subplots()
    for spine in ["left", "bottom"]:
        ax.spines[spine].set_position("zero")

    for spine in ["right", "top"]:
        ax.spines[spine].set_color("none")

    return ax

def vect_fig(vector, color):
    """Genera el grafico de los vectores en el plano"""
    v = vector
    ax.annotate(" ", xy=v, xytext=[0, 0], color=color,
                arrowprops=dict(facecolor=color,
                                shrink=0,
                                alpha=0.7,
                                width=0.5))
    ax.text(1.1 * v[0], 1.1 * v[1], v)

ax = move_spines()
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.grid()
vect_fig([2, 4], "blue")

Combinaciones lineales#

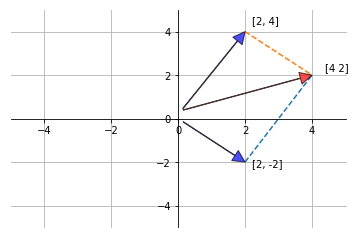
Cuando trabajamos con vectores, nos vamos a encontrar con dos operaciones fundamentales, la suma o adición; y la multiplicación por escalares. Cuando sumamos dos vectores $v$ y $w$, sumamos elemento por elemento, del siguiente modo:

Geométricamente lo podemos ver representado del siguiente modo:

# <!-- collapse=True -->
# graficando suma de vectores en R^2
# [2, 4] + [2, -2]

ax = move_spines()
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.grid()
vecs = [[2, 4], [2, -2]] # lista de vectores
for v in vecs:
    vect_fig(v, "blue")

v = np.array([2, 4]) + np.array([2, -2])
vect_fig(v, "red")

ax.plot([2, 4], [-2, 2], linestyle='--')
a =ax.plot([2, 4], [4, 2], linestyle='--' )

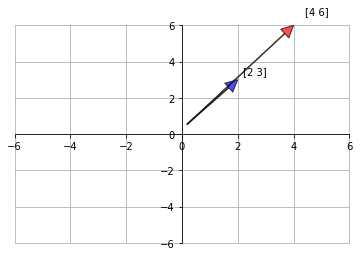
Cuando multiplicamos vectores por escalares, lo que hacemos es tomar un número $\alpha$ y un vector $v$; y creamos un nuevo vector $w$ en el cada elemento de $v$ es multiplicado por $\alpha$ del siguiente modo:

Geométricamente podemos representar a esta operación en el plano de 2 dimensiones del siguiente modo:

# <!-- collapse=True -->
# graficando multiplicación por escalares en R^2
# [2, 3] * 2

ax = move_spines()
ax.set_xlim(-6, 6)
ax.set_ylim(-6, 6)
ax.grid()

v = np.array([2, 3])
vect_fig(v, "blue")

v = v * 2
vect_fig(v, "red")

Cuando combinamos estas dos operaciones, formamos lo que se conoce en Álgebra lineal como combinaciones lineales. Es decir que una combinación lineal va a ser una expresión matemática construida sobre un conjunto de vectores, en el que cada vector es multiplicado por un escalar y los resultados son luego sumados. Matemáticamente lo podemos expresar de la siguiente forma:

en donde, $v_n$ son vectores y ${\alpha }_n$ son escalares.

Matrices, combinaciones lineales y Ax = b#

Una matriz es un arreglo bidimensional de números ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. En una matriz cada elemento puede ser identificado utilizando dos índices, uno para la fila y otro para la columna en que se encuentra. Las podemos representar de la siguiente manera:

Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar combinaciones lineales.

Supongamos que tenemos los siguientes 3 vectores:

su combinación lineal en el espacio de 3 dimensiones va a ser igual a ${\alpha }_1{x}_1+{\alpha }_2{x}_2+{\alpha }_3{x}_3$; lo que es lo mismo que decir:

Ahora esta combinación lineal la podríamos reescribir en forma matricial. Los vectores $x_1,x_2$ y $x_3$, pasarían a formar las columnas de la matriz $A$ y los escalares ${\alpha }_1,{\alpha }_2$ y ${\alpha }_3$ pasarían a ser los componentes del vector $x$ del siguiente modo:

De esta forma la matriz $A$ multiplicada por el vector $x$, nos da como resultado la misma combinación lineal $b$. De esta forma, arribamos a una de las ecuaciones más fundamentales del Álgebra lineal:

Esta ecuación no solo nos va a servir para expresar combinaciones lineales, sino que también se vuelve de suma importancia a la hora de resolver sistemas de ecuaciones lineales, en dónde $b$ va a ser conocido y la incógnita pasa a ser $x$. Por ejemplo, supongamos que queremos resolver el siguiente sistemas de ecuaciones de 3 incógnitas:

Podemos ayudarnos de SymPy para expresar a la matriz $A$ y $b$ para luego arribar a la solución del vector $x$.

# Resolviendo sistema de ecuaciones con SymPy
A = sympy.Matrix(( (2, 3, 5), (3, 6, 2), (8, 3, 6) ))
A

b = sympy.Matrix(3,1,(52,61,75))
b

# Resolviendo Ax = b
x = A.LUsolve(b)
x

# Comprobando la solución
A*x

La matriz identidad , la matriz transpuesta y la matriz invertible#

Tres matrices de suma importancia en problemas de Álgebra lineal. Son la matriz identidad, la matriz transpuesta y la matriz invertible.

La matriz identidad es el elemento neutro en la multiplicación de matrices, es el equivalente al número 1. Cualquier matriz multiplicada por la matriz identidad nos da como resultado la misma matriz. La matriz identidad es una matriz cuadrada (tiene siempre el mismo número de filas que de columnas); y su diagonal principal se compone de todos elementos 1 y el resto de los elementos se completan con 0. Suele representase con la letra $I$.

Por ejemplo la matriz identidad de 3x3 sería la siguiente:

La matriz transpuesta de una matriz $A$ de $m\times n$ va a ser igual a la matriz $n\times m$ $A^T$, la cual se obtiene al transformar las filas en columnas y las columnas en filas, del siguiente modo:

Una matriz cuadrada va a ser simétrica si $A^T=A$, es decir si $A$ es igual a su propia matriz transpuesta.

Algunas de las propiedades de las matrices transpuestas son:

a. $(A^T{)}^T=A$

b. $(A+B{)}^T=A^T+B^T$

c. $k(A{)}^T=k(A^T)$

d. $(AB{)}^T=B^T{A}^T$

e. $(A^r{)}^T=(A^T{)}^r$ para todos los $r$ no negativos.

f. Si $A$ es una matriz cuadrada, entonces $A+A^T$ es una matriz simétrica.

g. Para cualquier matriz $A$, $A{A}^T$ y $A^{T}A$ son matrices simétricas.

Veamos algunos ejemplos en Python

# Matriz transpuesta
A = sympy.Matrix( [[ 2,-3,-8, 7],
                   [-2,-1, 2,-7],
                   [ 1, 0,-3, 6]] )
A

A.transpose()

# transpuesta de transpuesta vuelve a A.
A.transpose().transpose()

# creando matriz simetrica
As = A*A.transpose()
As

# comprobando simetria.
As.transpose()

La matriz invertible es muy importante, ya que esta relacionada con la ecuación $Ax=b$. Si tenemos una matriz cuadrada $A$ de $n\times n$, entonces la matriz inversa de $A$ es una matriz $A^{\prime }$ o $A^{-1}$ de $n\times n$ que hace que la multiplicación $A{A}^{-1}$ sea igual a la matriz identidad $I$. Es decir que es la matriz recíproca de $A$.

$A{A}^{-1}=I$ o $A^{-1}A=I$

En caso de que estas condiciones se cumplan, decimos que la matriz es invertible.

Que una matriz sea invertible tiene importantes implicaciones, como ser:

a. Si $A$ es una matriz invertible, entonces su matriz inversa es única.

b. Si $A$ es una matriz invertible de $n\times n$, entonces el sistemas de ecuaciones lineales dado por $Ax=b$ tiene una única solución $x=A^{-1}b$ para cualquier $b$ en ${\mathbb{R}}^n$.

c. Una matriz va a ser invertible si y solo si su determinante es distinto de cero. En el caso de que el determinante sea cero se dice que la matriz es singular.

d. Si $A$ es una matriz invertible, entonces el sistema $Ax=0$ solo tiene una solución trivial. Es decir, en las que todas las incógnitas son ceros.

e. Si $A$ es una matriz invertible, entonces su forma escalonada va a ser igual a la matriz identidad.

f. Si $A$ es una matriz invertible, entonces $A^{-1}$ es invertible y:

g. Si $A$ es una matriz invertible y $\alpha$ es un escalar distinto de cero, entonces $\alpha A$ es invertible y:

.

h. Si $A$ y $B$ son matrices invertibles del mismo tamaño, entonces $AB$ es invertible y:

.

i. Si $A$ es una matriz invertible, entonces $A^T$ es invertible y:

.

Con SymPy podemos trabajar con las matrices invertibles del siguiente modo:

# Matriz invertible
A = sympy.Matrix( [[1,2],
                   [3,9]] )
A

A_inv = A.inv()
A_inv

# A * A_inv = I
A*A_inv

# forma escalonada igual a indentidad.
A.rref()

# la inversa de A_inv es A
A_inv.inv()

Espacios vectoriales#

Las Matemáticas derivan su poder en gran medida de su capacidad para encontrar las características comunes de los diversos problemas y estudiarlos de manera abstracta. Existen muchos problemas que implican los conceptos relacionados de adición, multiplicación por escalares, y la linealidad. Para estudiar estas propiedades de manera abstracta, debemos introducir la noción de espacio vectorial.

Para alcanzar la definición de un espacio vectorial, debemos combinar los conceptos que venimos viendo hasta ahora de Campo, vector y las operaciones de adición; y multiplicación por escalares. De esta forma un espacio vectorial, $V$, sobre un Campo, $F$, va a ser un conjunto en el que están definidas las operaciones de adición y multiplicación por escalares, tal que para cualquier par de elementos $x$ e $y$ en $V$, existe un elemento único $x+y$ en $V$, y para cada elemento $\alpha$ en $F$ y cada elemento $x$ en $V$, exista un único elemento $\alpha x$ en $V$, de manera que se cumplan las siguientes condiciones:

1. Para todo $x,y$ en $V$, $x+y=y+x$ (conmutatividad de la adición).

2. Para todo $x,y,z$ en $V$, $(x+y)+z=x+(y+z)$. (asociatividad de la adición).

3. Existe un elemento en $V$ llamado $0$ tal que $x+0=x$ para todo $x$ en $V$.

4. Para cada elemento $x$ en $V$, existe un elemento $y$ en $V$ tal que $x+y=0$.

5. Para cada elemento $x$ en $V$, $1x=x$.

6. Para cada par, $\alpha ,\beta$ en $F$ y cada elemento $x$ en $V$, $(\alpha \beta )x=\alpha (\beta x)$.

7. Para cada elemento $\alpha$ en $F$ y cada para de elementos $x,y$ en $V$, $\alpha (x+y)=\alpha x+\alpha y$.

8. Para cada par de elementos $\alpha ,\beta$ en $F$ y cada elemento $x$ en $V$, $(\alpha +\beta )x=\alpha x+\beta x$.

Los espacios vectoriales más comunes son ${\mathbb{R}}^2$, el cual representa el plano de 2 dimensiones y consiste de todos los pares ordenados de los números reales:

y ${\mathbb{R}}^3$, que representa el espacio ordinario de 3 dimensiones y consiste en todos los tríos ordenados de los números reales:

Una de las grandes bellezas del Álgebra lineal es que podemos fácilmente pasar a trabajar sobre espacios de $n$ dimensiones, ${\mathbb{R}}^n$!

Tampoco tenemos porque quedarnos con solo los números reales, ya que la definición que dimos de un espacio vectorial reside sobre un Campo; y los campos pueden estar representados por números complejos. Por tanto también podemos tener espacios vectoriales ${\mathbb{C}}^2,{\mathbb{C}}^3,\dots ,{\mathbb{C}}^n$.

Subespacios#

Normalmente, en el estudio de cualquier estructura algebraica es interesante examinar subconjuntos que tengan la misma estructura que el conjunto que esta siendo considerado. Así, dentro de los espacios vectoriales, podemos tener subespacios vectoriales, los cuales son un subconjunto que cumplen con las mismas propiedades que el espacio vectorial que los contiene. De esta forma, ${\mathbb{R}}^3$ representa un subespacio del espacio vectorial ${\mathbb{R}}^n$.

Independencia lineal#

La independencia lineal es un concepto aparentemente simple con consecuencias que se extienden profundamente en muchos aspectos del análisis. Si deseamos entender cuando una matriz puede ser invertible, o cuando un sistema de ecuaciones lineales tiene una única solución, o cuando una estimación por mínimos cuadrados se define de forma única, la idea fundamental más importante es la de independencia lineal de vectores.

Dado un conjunto finito de vectores $x_1,x_2,\dots ,x_n$ se dice que los mismos son linealmente independientes, si y solo si, los únicos escalares ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ que satisfacen la ecuación:

son todos ceros, ${\alpha }_1={\alpha }_2=\cdots ={\alpha }_n=0$.

En caso de que esto no se cumpla, es decir, que existe una solución a la ecuación de arriba en que no todos los escalares son ceros, a esta solución se la llama no trivial y se dice que los vectores son linealmente dependientes.

Para ilustrar la definición y que quede más clara, veamos algunos ejemplos. Supongamos que queremos determinar si los siguientes vectores son linealmente independientes:

Para lograr esto, deberíamos resolver el siguiente sistema de ecuaciones y verificar si la única solución es aquella en que los escalares sean ceros.

Para resolver este sistema de ecuaciones, podemos recurrir a la ayuda de Python.

# Resolviendo el sistema de ecuaciones.
A = np.array([[1.2, -2.2],
              [1.1, 1.4]])

b = np.array([0., 0.])

x = np.linalg.solve(A, b)
x

array([0., 0.])

# <!-- collapse=True -->
# Solución gráfica.
x_vals = np.linspace(-5, 5, 50) # crea 50 valores entre 0 y 5

ax = move_spines()
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.grid()

ax.plot(x_vals, (1.2 * x_vals) / -2.2) # grafica 1.2x_1 - 2.2x_2 = 0
a = ax.plot(x_vals, (1.1 * x_vals) / 1.4) # grafica 1.1x + 1.4x_2 = 0

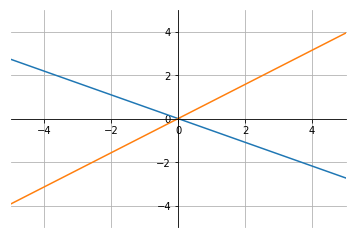
Como podemos ver, tanto por la solución numérica como por la solución gráfica, estos vectores son linealmente independientes, ya que la única solución a la ecuación ${\alpha }_1{x}_1+{\alpha }_2{x}_2+\cdots +{\alpha }_n{x}_n=0$, es aquella en que los escalares son cero.

Determinemos ahora si por ejemplo, los siguientes vectores en ${\mathbb{R}}^4$ son linealmente independientes: $(3,2,2,3),(3,2,1,2),(3,2,0,1)$. Aquí, ahora deberíamos resolver la siguiente ecuación:

Para resolver este sistema de ecuaciones que no es cuadrado (tiene 4 ecuaciones y solo 3 incógnitas); podemos utilizar SymPy.

# Sympy para resolver el sistema de ecuaciones lineales
a1, a2, a3 = sympy.symbols('a1, a2, a3')
A = sympy.Matrix(( (3, 3, 3, 0), (2, 2, 2, 0), (2, 1, 0, 0), (3, 2, 1, 0) ))
A

sympy.solve_linear_system(A, a1, a2, a3)

Como vemos, esta solución es no trivial, ya que por ejemplo existe la solución ${\alpha }_1=1,{\alpha }_2=-2,{\alpha }_3=1$ en la que los escalares no son ceros. Por lo tanto este sistema es linealmente dependiente.

Por último, podríamos considerar si los siguientes polinomios son linealmente independientes: $1-2x-x^2$, $1+x$, $1+x+2x^2$. En este caso, deberíamos resolver la siguiente ecuación:

y esta ecuación es equivalente a la siguiente:

Por lo tanto, podemos armar el siguiente sistema de ecuaciones:

El cual podemos nuevamente resolver con la ayuda de SymPy.

A = sympy.Matrix(( (1, 1, 1, 0), (-2, 1, 1, 0), (-1, 2, 0, 0) ))
A

sympy.solve_linear_system(A, a1, a2, a3)

Como vemos, todos los escalares son ceros, por lo tanto estos polinomios son linealmente independientes.

Espacio nulo, espacio columna y espacio fila#

Un termino particularmente relacionado con la independencia lineal es el de espacio nulo o núcleo. El espacio nulo de una matriz $A$, el cual lo vamos a expresar como $N(A)$, va a consistir de todas las soluciones a la ecuación fundamental $Ax=0$. Por supuesto, una solución inmediata a esta ecuación es el caso de $x=0$, que ya vimos que establece la independencia lineal. Esta solución solo va a ser la única que exista para los casos de matrices invertibles. Pero en el caso de las matrices singulares (aquellas que no son invertibles, que tienen determinante igual a cero), van a existir soluciones que no son cero para la ecuación $Ax=0$. El conjunto de todas estas soluciones, va a representar el espacio nulo.

Para encontrar el espacio nulo también nos podemos ayudar de SymPy.

# Espacio nulo de un matriz
A = sympy.Matrix(((1, 5, 7), (0, 0, 9)))
A

# Calculando el espacio nulo
x = A.nullspace()
x

# Comprobando la solución
A_aum = sympy.Matrix(((1, 5, 7, 0), (0, 0, 9, 0)))
sympy.solve_linear_system(A_aum, a1, a2, a3)

# Comprobación con numpy
A = np.array([[1, 5, 7],
               [0, 0, 9]])
x = np.array([[-5],
               [1],
               [0]])

A.dot(x)

array([[0],
       [0]])

Otro espacio de suma importancia es el espacio columna. El espacio columna, $C(A)$, consiste en todas las combinaciones lineales de las columnas de una matriz $A$. Estas combinaciones son los posibles vectores $Ax$. Este espacio es fundamental para resolver la ecuación $Ax=b$; ya que para resolver esta ecuación debemos expresar a $b$ como una combinación de columnas. El sistema $Ax=b$, va a tener solución solamente si $b$ esta en el espacio columna de $A$. Como las matrices tienen la forma $m\times n$, sus columnas tienen $m$ componentes ($n$ son las filas). Por lo tanto el espacio columna es un subespacio de ${\mathbb{R}}^m$ y no ${\mathbb{R}}^n$.

Por último, el otro espacio que conforma los espacios fundamentales de una matriz, es el espacio fila, el cual esta constituido por las combinaciones lineales de las filas de una matriz.

Para obtener estos espacios, nuevamente podemos recurrir a SymPy. Para poder obtener estos espacios, primero vamos a tener que obtener la forma escalonada de la matriz, la cual es la forma a la que arribamos luego del proceso de eliminación.

# A.rref() forma escalonada.
A = sympy.Matrix( [[2,-3,-8, 7],
                   [-2,-1,2,-7],
                   [1 ,0,-3, 6]])

A.rref() # [0, 1, 2] es la ubicación de las pivot.

# Espacio columna
[ A[:,c] for c in A.rref()[1] ]

# Espacio fila
[ A.rref()[0][r,:] for r in A.rref()[1] ]

Rango#

Otro concepto que también esta ligado a la independencia lineal es el de rango. Los números de columnas $m$ y filas $n$ pueden darnos el tamaño de una matriz, pero esto no necesariamente representa el verdadero tamaño del sistema lineal, ya que por ejemplo si existen dos filas iguales en una matriz $A$, la segunda fila desaparecía en el proceso de eliminación. El verdadero tamaño de $A$ va a estar dado por su rango. El rango de una matriz es el número máximo de columnas (filas respectivamente) que son linealmente independientes. Por ejemplo si tenemos la siguiente matriz de 3 x 4:

Podemos ver que la tercer columna $(2,2,2)$ es un múltiplo de la primera y que la cuarta columna $(4,5,6)$ es la suma de las primeras 3 columnas. Por tanto el rango de $A$ va a ser igual a 2; ya que la tercer y cuarta columna pueden ser eliminadas.

Obviamente, el rango también lo podemos calcular con la ayuda de Python.

# Calculando el rango con SymPy
A = sympy.Matrix([[1, 1, 2, 4],
                  [1, 2, 2, 5],
                  [1, 3, 2, 6]])
A

# Rango con SymPy
A.rank()

# Rango con numpy
A = np.array([[1, 1, 2, 4],
              [1, 2, 2, 5],
              [1, 3, 2, 6]])
np.linalg.matrix_rank(A)

2

Una útil aplicación de calcular el rango de una matriz es la de determinar el número de soluciones al sistema de ecuaciones lineales, de acuerdo al enunciado del Teorema de Rouché–Frobenius. El sistema tiene por lo menos una solución si el rango de la matriz de coeficientes equivale al rango de la matriz aumentada. En ese caso, ésta tiene exactamente una solución si el rango equivale al número de incógnitas.

La norma y la Ortogonalidad#

Si quisiéramos saber cual es el largo del un vector, lo único que necesitamos es el famoso teorema de Pitágoras. En el plano ${\mathbb{R}}^2$, el largo de un vector $v=\left[\begin{array}{c}ab\end{array}\right]$ va a ser igual a la distancia desde el origen $(0,0)$ hasta el punto $(a,b)$. Esta distancia puede ser fácilmente calculada gracias al teorema de Pitágoras y va ser igual a $\sqrt{a^2+b^2}$, como se puede ver en la siguiente figura:

# <!-- collapse=True -->
# Calculando largo de un vector
# forma un triángulo rectángulo

ax = move_spines()
ax.set_xlim(-6, 6)
ax.set_ylim(-6, 6)
ax.grid()
v = np.array([4, 6])

vect_fig(v, "blue")

a = ax.vlines(x=v[0], ymin=0, ymax = 6, linestyle='--', color='g')

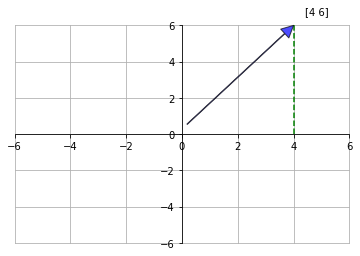
En esta definición podemos observar que $a^2+b^2=v\cdot v$, por lo que ya estamos en condiciones de poder definir lo que en Álgebra lineal se conoce como norma.

El largo o norma de un vector $v=\left[\begin{array}{c}{v}_1{v}_2⋮v_n\end{array}\right]$, en ${\mathbb{R}}^n$ va a ser igual a un número no negativo $||v||$ definido por:

Es decir que la norma de un vector va a ser igual a la raíz cuadrada de la suma de los cuadrados de sus componentes.

Ortogonalidad#

El concepto de perpendicularidad es fundamental en geometría. Este concepto llevado a los vectores en ${\mathbb{R}}^n$ se llama ortogonalidad.

Dos vectores $v$ y $w$ en ${\mathbb{R}}^n$ van a ser ortogonales el uno al otro si su producto interior es igual a cero. Es decir, $v\cdot w=0$.

Geométricamente lo podemos ver de la siguiente manera:

# <!-- collapse=True -->
# Vectores ortogonales

ax = move_spines()
ax.set_xlim(-6, 6)
ax.set_ylim(-6, 6)
ax.grid()
vecs = [np.array([4, 6]), np.array([-3, 2])]

for v in vecs:
    vect_fig(v, "blue")

a = ax.plot([-3, 4], [2, 6], linestyle='--', color='g')

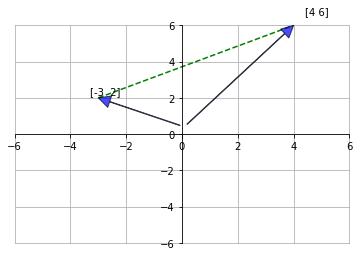
# comprobando su producto interior.
v = np.array([4, 6])
w = np.array([-3, 2])
v.dot(w)

0

Un conjunto de vectores en ${\mathbb{R}}^n$ va a ser ortogonal si todo los pares de los distintos vectores en el conjunto son ortogonales entre sí. O sea:

$v_i\cdot v_j=0$ para todo $i,j=1,2,\dots ,k$ y donde $i\ne j$.

Por ejemplo, si tenemos el siguiente conjunto de vectores en ${\mathbb{R}}^3$:

En este caso, deberíamos combrobar que:

# comprobando ortogonalidad del conjunto

v1 = np.array([2, 1, -1])
v2 = np.array([0, 1, 1])
v3 = np.array([1, -1, 1])

v1.dot(v2), v2.dot(v3), v1.dot(v3)

(0, 0, 0)

Como vemos, este conjunto es ortogonal. Una de las principales ventajas de trabajar con conjuntos de vectores ortogonales es que los mismos son necesariamente linealmente independientes.

El concepto de ortogonalidad es uno de los más importantes y útiles en Álgebra lineal y surge en muchas situaciones prácticas, sobre todo cuando queremos calcular distancias.

Determinante#

El determinante es un número especial que puede calcularse sobre las matrices cuadradas. Este número nos va a decir muchas cosas sobre la matriz. Por ejemplo, nos va decir si la matriz es invertible o no. Si el determinante es igual a cero, la matriz no es invertible. Cuando la matriz es invertible, el determinante de $A^{-1}=1/(detA)$. El determinante también puede ser útil para calcular áreas.

Para obtener el determinante de una matriz debemos calcular la suma de los productos de las diagonales de la matriz en una dirección menos la suma de los productos de las diagonales en la otra dirección. Se represente con el símbolo $|A|$ o $detA$.

Algunas de sus propiedades que debemos tener en cuenta son:

a. El determinante de la matriz identidad es igual a 1. $detI=1$.

b. Una matriz $A$ es singular (no tiene inversa) si su determinante es igual a cero.

c. El determinante cambia de signo cuando dos columnas(o filas) son intercambiadas.

d. Si dos filas de una matriz $A$ son iguales, entonces el determinante es cero.

e. Si alguna fila de la matriz $A$ son todos ceros, entonces el determinante es cero.

f. La matriz transpuesta $A^T$, tiene el mismo determinante que $A$.

g. El determinante de $AB$ es igual al determinante de $A$ multiplicado por el determinante de $B$. $det(AB)=detA\cdot detB$.

h. El determinante es una función lineal de cada una de las filas en forma separada. Si multiplicamos solo una fila por $\alpha$, entonces el determinante también es multiplicado por $\alpha$.

Veamos como podemos obtener el determinante con la ayuda de Python

# Determinante con sympy
A = sympy.Matrix( [[1, 2, 3],
                   [2,-2, 4],
                   [2, 2, 5]] )
A.det()

# Determinante con numpy
A = np.array([[1, 2, 3],
              [2,-2, 4],
              [2, 2, 5]] )
np.linalg.det(A)

# Determinante como funcion lineal de fila
A[0] = A[0:1]*5
np.linalg.det(A)

# cambio de signo de determinante
A = sympy.Matrix( [[2,-2, 4],
                   [1, 2, 3],
                   [2, 2, 5]] )
A.det()

Eigenvalores y Eigenvectores#

Cuando estamos resolviendo ecuaciones lineales del tipo $Ax=b$, estamos trabajando con problemas estáticos. ¿Pero qué pasa si quisiéramos trabajar con problemas dinámicos?. Es en este tipo de situaciones donde los Eigenvalores y Eigenvectores tienen su mayor importancia.

Supongamos que tenemos una matriz cuadrada $A$ de $n\times n$. Una pregunta natural que nos podríamos hacer sobre $A$ es: ¿Existe algún vector $x$ distinto de cero para el cual $Ax$ es un escalar múltiplo de $x$?. Si llevamos esta pregunta al lenguaje matemático nos vamos a encontrar con la siguiente ecuación:

Cuando esta ecuación es válida y $x$ no es cero, decimos que $\lambda$ es el Eigenvalor o valor propio de $A$ y $x$ es su correspondiente Eigenvector o vector propio.

Muchos problemas en ciencia derivan en problemas de Eigenvalores, en los cuales la principal pregunta es: ¿Cuáles son los Eigenvalores de una matriz dada, y cuáles son sus correspondientes Eigenvectores. Un área donde nos va a ser de mucha utilidad esta teoría, es en problemas con sistemas de ecuaciones diferenciales lineales.

Calculando Eigenvalores#

Hasta aquí todo muy bien, pero dada una matriz cuadrada $A$ de $n\times n$, ¿cómo podemos obtener sus Eigenvalores?.

Podemos comenzar por observar que la ecuación $Ax=\lambda x$ es equivalente a $(A-\lambda I)x=0$. Dado que estamos interesados en soluciones a esta ecuación que sean distintas de cero, la matriz $A-\lambda I$ debe ser singular, no invertible, por lo tanto su determinante debe ser cero, $det(A-\lambda I)=0$. De esta forma, podemos utilizar esta ecuación para encontrar los Eigenvalores de $A$. Particularmente, podríamos formar el polinomio característico de la matriz $A$, el cual va a tener grado $n$ y por lo tanto va a tener $n$ soluciones, es decir que vamos a encontrar $n$ Eigenvalores. Algo que debemos tener en cuenta es, que a pesar de que la matriz $A$ sea real, debemos estar preparados para encontrar Eigenvalores que sean complejos.

Para que quede más claro, veamos un ejemplo de como podemos calcular los Eigenvalores. Supongamos que tenemos la siguiente matriz:

Su polinomio característico va a ser igual a:

Por lo tanto los Eigenvalores de $A$ van a ser $5$ y $-4$.

Obviamente, también los podemos obtener mucho más fácilmente con la ayuda de Python.

# Eigenvalores con numpy
A = np.array([[3, 2],
              [7, -2]])

x, v = np.linalg.eig(A)

# x Eigenvalor, v Eigenvector
x, v

(array([ 5., -4.]), array([[ 0.70710678, -0.27472113],
        [ 0.70710678,  0.96152395]]))

# Eigenvalores con SymPy
A = sympy.Matrix([[3, 2],
                  [7, -2]])

# Eigenvalor
A.eigenvals()

# Eigenvector
A.eigenvects()

# comprobando la solución Ax = λx
# x eigenvector, v eigenvalue
x = A.eigenvects()[0][2][0]
v = A.eigenvects()[0][0]

# Ax == vx
A*x, v*x

Con esto termino con este recorrido por los principales conceptos del Álgebra lineal, muchos de los cuales veremos en próximos artículos que tienen muchas aplicaciones interesantes. Espero que les sea de utilidad y les sirva de referencia.

Saludos!

Este post fue escrito utilizando Jupyter notebook. Pueden descargar este notebook o ver su version estática en nbviewer.