Redes neuronales convolucionales con TensorFlow
Esta notebook fue creada originalmente como un blog post por Raúl E. López Briega en Matemáticas, Analisis de datos y Python. El contenido esta bajo la licencia BSD.

Introducción
De más esta decir que el sentido de la visión es uno de los grandes prodigios de la Naturaleza. En fracciones de segundos, podemos identificar objetos dentro de nuestro campo de visión, sin siquiera detenernos a pensar en ello. Pero no sólo podemos nombrar estos objetos que observamos, sino que también podemos percibir su profundidad, distinguir perfectamente sus contornos, y separarlos de sus fondos. De alguna manera los ojos captan datos de píxeles, pero el cerebro transforma esa información en características más significativas - líneas, curvas y formas - que podrían indicar, por ejemplo, que estamos mirando a una persona.
Gracias a que el área del cerebro responsable de la visión es una de las zonas más estudiadas y que más conocemos; sabemos que la corteza visual contiene una disposición jerárquica compleja de neuronas. Por ejemplo, la información visual es introducida en la corteza a través del área visual primaria, llamada V1. Las neuronas de V1 se ocupan de características visuales de bajo nivel, tales como pequeños segmentos de contorno, componentes de pequeña escala del movimiento, disparidad binocular, e información básica de contraste y color. V1 luego alimenta de información a otras áreas, como V2, V4 y V5. Cada una de estas áreas se ocupa de los aspectos más específicos o abstractas de la información. Por ejemplo, las neuronas en V4 se ocupan de objetos de mediana complejidad, tales como formas de estrellas en diferentes colores. La corteza visual de los animales es el más potente sistema de procesamiento visual que conocemos, por lo que suena lógico inspirarse en ella para crear una variante de redes neuronales artificiales que ayude a identificar imágenes; es así como surgen las redes neuronales convolucionales.
¿Qué son las Redes Neuronales Convolucionales?
Las redes neuronales convolucionales son muy similares a las redes neuronales ordinarias como el perceptron multicapa que vimos en el artículo anterior; se componen de neuronas que tienen pesos y sesgos que pueden aprender. Cada neurona recibe algunas entradas, realiza un producto escalar y luego aplica una función de activación. Al igual que en el perceptron multicapa también vamos a tener una función de pérdida o costo (por ejemplo SVM / Softmax) sobre la última capa, la cual estará totalmente conectada. Lo que diferencia a las redes neuronales convolucionales es que suponen explícitamente que las entradas son imágenes, lo que nos permite codificar ciertas propiedades en la arquitectura; permitiendo ganar en eficiencia y reducir la cantidad de parámetros en la red. Las redes neuronales convolucionales vienen a solucionar el problema de que las redes neuronales ordinarias no escalan bien para imágenes de mucha definición; por ejemplo en el problema de MNIST, las imágenes son de 28x28; por lo que una sola neurona plenamente conectado en una primera capa oculta de una red neuronal ordinaria tendría 28 x 28 = 784 pesos. Esta cantidad todavía parece manejable, pero es evidente que esta estructura totalmente conectado no funciona bien con imágenes más grandes. Si tomamos el caso de una imagen de mayor tamaño, por ejemplo de 200x200 con colores RGB, daría lugar a neuronas que tienen 200 x 200 x 3 = 120.000 pesos. Por otra parte, el contar con tantos parámetros, también sería un desperdicio de recursos y conduciría rápidamente a sobreajuste.
Las redes neuronales convolucionales trabajan modelando de forma consecutiva pequeñas piezas de información, y luego combinando esta información en las capas más profundas de la red. Una manera de entenderlas es que la primera capa intentará detectar los bordes y establecer patrones de detección de bordes. Luego, las capas posteriores trataran de combinarlos en formas más simples y, finalmente, en patrones de las diferentes posiciones de los objetos, iluminación, escalas, etc. Las capas finales intentarán hacer coincidir una imagen de entrada con todas los patrones y arribar a una predicción final como una suma ponderada de todos ellos. De esta forma las redes neuronales convolucionales son capaces de modelar complejas variaciones y comportamientos dando predicciones bastantes precisas.
Estructura de las Redes Neuronales Convolucionales
En general, las redes neuronales convolucionales van a estar construidas con una estructura que contendrá 3 tipos distintos de capas:
- Una capa convolucional, que es la que le da le nombre a la red.
- Una capa de reducción o de pooling, la cual va a reducir la cantidad de parámetros al quedarse con las características más comunes.
- Una capa clasificadora totalmente conectada, la cual nos va dar el resultado final de la red.
Profundicemos un poco en cada una de ellas.
Capa convolucional
Como dijimos anteriormente, lo que distingue a las redes neuronales convolucionales de cualquier otra red neuronal es utilizan un operación llamada convolución en alguna de sus capas; en lugar de utilizar la multiplicación de matrices que se aplica generalmente. La operación de convolución recibe como entrada o input la imagen y luego aplica sobre ella un filtro o kernel que nos devuelve un mapa de las características de la imagen original, de esta forma logramos reducir el tamaño de los parámetros. La convolución aprovecha tres ideas importantes que pueden ayudar a mejorar cualquier sistema de machine learning, ellas son:
- interacciones dispersas, ya que al aplicar un filtro de menor tamaño sobre la entrada original podemos reducir drásticamente la cantidad de parámetros y cálculos;
- los parámetros compartidos, que hace referencia a compartir los parámetros entre los distintos tipos de filtros, ayudando también a mejorar la eficiencia del sistema; y
- las representaciones equivariante, que indican que si las entradas cambian, las salidas van a cambiar también en forma similar.
Por otra parte, la convolución proporciona un medio para trabajar con entradas de tamaño variable, lo que puede ser también muy conveniente.

Capa de reducción o pooling
La capa de reducción o pooling se coloca generalmente después de la capa convolucional. Su utilidad principal radica en la reducción de las dimensiones espaciales (ancho x alto) del volumen de entrada para la siguiente capa convolucional. No afecta a la dimensión de profundidad del volumen. La operación realizada por esta capa también se llama reducción de muestreo, ya que la reducción de tamaño conduce también a la pérdida de información. Sin embargo, una pérdida de este tipo puede ser beneficioso para la red por dos razones:
- la disminución en el tamaño conduce a una menor sobrecarga de cálculo para las próximas capas de la red;
- también trabaja para reducir el sobreajuste.
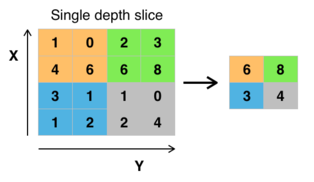
La operación que se suele utilizar en esta capa es max-pooling, que divide a la imagen de entrada en un conjunto de rectángulos y, respecto de cada subregión, se va quedando con el máximo valor.
Capa clasificadora totalmente conectada
Al final de las capas convolucional y de pooling, las redes utilizan generalmente capas completamente conectados en la que cada pixel se considera como una neurona separada al igual que en una red neuronal regular. Esta última capa clasificadora tendrá tantas neuronas como el número de clases que se debe predecir.
Ejemplo en TensorFlow
Luego de toda esta introducción teórica es tiempo de pasar a la acción y ver como podemos aplicar todo lo que hemos aprendimos para crear una red neuronal convolucional con la ayuda de TensorFlow. Para esto vamos volver a utilizar el conjunto de datos MNIST, pero esta vez vamos a clasificar los digitos utilizando una red neuronal convolucional.
# importamos la libreria
import tensorflow as tf
# importando el dataset
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
# Parametros
tasa_aprendizaje = 0.001
epocas = 200000
lote = 128
mostrar_paso = 100
# Parametros de la red
n_entradas = 784 # datos de MNIST(forma img: 28*28)
n_clases = 10 # Total de clases a clasificar (0-9 digitos)
dropout = 0.75 # Dropout, probabilidad para quedarse con unidades
# input para los grafos
x = tf.placeholder(tf.float32, [None, n_entradas])
y = tf.placeholder(tf.float32, [None, n_clases])
keep_prob = tf.placeholder(tf.float32) #dropout
# Creación del modelo
def conv2d(x, W, b, strides=1):
# capa convolucional con activacion relu
x = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='SAME')
x = tf.nn.bias_add(x, b)
return tf.nn.relu(x)
def maxpool2d(x, k=2):
# capa de pooling con max pooling
return tf.nn.max_pool(x, ksize=[1, k, k, 1], strides=[1, k, k, 1],
padding='SAME')
# armado de la red
def conv_net(x, weights, biases, dropout):
# cambiar la forma de la imagen
x = tf.reshape(x, shape=[-1, 28, 28, 1])
# capa convolucional
conv1 = conv2d(x, pesos['pc1'], sesgo['sc1'])
# Max Pooling (reducción de muestreo)
conv1 = maxpool2d(conv1, k=2)
# capa convolucional
conv2 = conv2d(conv1, pesos['pc2'], sesgo['sc2'])
# Max Pooling (reducción de muestreo)
conv2 = maxpool2d(conv2, k=2)
# capa clasificadora totalmente conectada
fc1 = tf.reshape(conv2, [-1, pesos['pd1'].get_shape().as_list()[0]])
fc1 = tf.add(tf.matmul(fc1, pesos['pd1']), sesgo['sd1'])
fc1 = tf.nn.relu(fc1)
# aplicar descarte
fc1 = tf.nn.dropout(fc1, dropout)
# Output, prediccion de la clase
out = tf.add(tf.matmul(fc1, pesos['out']), sesgo['out'])
return out
# Definimos los pesos y sesgo de cada capa
pesos = {
# 5x5 conv, 1 input, 32 outputs
'pc1': tf.Variable(tf.random_normal([5, 5, 1, 32])),
# 5x5 conv, 32 inputs, 64 outputs
'pc2': tf.Variable(tf.random_normal([5, 5, 32, 64])),
# totalmente conectada, 7*7*64 inputs, 1024 outputs
'pd1': tf.Variable(tf.random_normal([7*7*64, 1024])),
# 1024 inputs, 10 outputs (prediccion de clase)
'out': tf.Variable(tf.random_normal([1024, n_clases]))
}
sesgo = {
'sc1': tf.Variable(tf.random_normal([32])),
'sc2': tf.Variable(tf.random_normal([64])),
'sd1': tf.Variable(tf.random_normal([1024])),
'out': tf.Variable(tf.random_normal([n_clases]))
}
# Construct model
pred = conv_net(x, pesos, sesgo, keep_prob)
# Define loss and optimizer
costo = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, y))
optimizador = tf.train.AdamOptimizer(learning_rate=tasa_aprendizaje
).minimize(costo)
# Evaluate model
pred_correcta = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
precision = tf.reduce_mean(tf.cast(pred_correcta, tf.float32))
# Initializing the variables
init = tf.initialize_all_variables()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
paso = 1
# Keep training until reach max iterations
while paso * lote < epocas:
batch_x, batch_y = mnist.train.next_batch(lote)
# Run optimization op (backprop)
sess.run(optimizador, feed_dict={x: batch_x, y: batch_y,
keep_prob: dropout})
if paso % mostrar_paso == 0:
# Calculate batch loss and accuracy
loss, acc = sess.run([costo, precision], feed_dict={x: batch_x,
y: batch_y,
keep_prob: 1.})
print("Iteración: {0: 04d} costo = {1:.6f} precision = {2:.5f}"
.format(paso*lote, loss, acc))
paso += 1
print("Optimización terminada!")
# Calculala precisión sobre los datos de evaluación
print("Precisión evalución: {0:.2f}".format(
sess.run(precision, feed_dict={x: mnist.test.images[:256],
y: mnist.test.labels[:256],
keep_prob: 1.})))
Iteración: 12800 costo = 4224.402344 precision = 0.78906
Iteración: 25600 costo = 1844.304932 precision = 0.89844
Iteración: 38400 costo = 289.222961 precision = 0.95312
Iteración: 51200 costo = 442.070557 precision = 0.95312
Iteración: 64000 costo = 275.925751 precision = 0.96094
Iteración: 76800 costo = 124.911362 precision = 0.96875
Iteración: 89600 costo = 302.610291 precision = 0.96875
Iteración: 102400 costo = 377.000092 precision = 0.95312
Iteración: 115200 costo = 348.436188 precision = 0.99219
Iteración: 128000 costo = 131.974304 precision = 0.99219
Iteración: 140800 costo = 442.505676 precision = 0.96875
Iteración: 153600 costo = 10.694885 precision = 0.98438
Iteración: 166400 costo = 39.013718 precision = 0.98438
Iteración: 179200 costo = 278.081543 precision = 0.96094
Iteración: 192000 costo = 91.298866 precision = 0.97656
Optimización terminada!
Precisión evalución: 0.98
Como podemos ver, utilizando redes neuronales convolucionales en lugar de un peceptron multicapa como hicimos en el artículo anterior; logramos una precisión de 98%, una mejora bastante significativa.
Aquí termina el artículo, espero que les haya resultado interesante y los motive a explorar el fascinante mundo de las redes neuronales.
Saludos!
Este post fue escrito utilizando IPython notebook. Pueden descargar este notebook o ver su version estática en nbviewer.