
Sobre TensoFlow¶
TensorFlow es una biblioteca open source desarrollada por Google que nos permite realizar cálculos numéricos usando diagramas de flujo de datos. Los nodos del grafo representan operaciones matemáticas, mientras que los arcos del grafo representan los arreglos de datos multidimensionales (tensores) comunicados entre ellos. Esta arquitectura flexible nos permite realizar los cálculos en más de un CPU o GPU utilizando la misma API.
¿Qué es un diagrama de flujo de datos?¶
Los diagramas de flujo de datos describen cálculos matemáticos con un grafo de nodos y arcos. Los nodos normalmente implementan operaciones matemáticas, pero también pueden representar los puntos para alimentarse de datos, devolver resultados, o leer / escribir variables persistentes. Los arcos o aristas describen las relaciones de entrada / salida entre los nodos. Estos arcos están representados por los arreglos de datos multidimensionales o tensores. El flujo de los tensores a través del grafo es de donde TensorFlow recibe su nombre. Los nodos se asignan a los dispositivos computacionales y se ejecutan de forma asincrónica y en paralelo una vez que todos los tensores en los arcos de entrada están disponibles.
Introducción a TensorFlow¶
Para poder utilizar TensorFlow primero es necesario entender cómo la librería:
- Representa cálculos en forma de grafos.
- Ejecuta los grafos en el contexto de Sesiones.
- Representa los datos como tensores.
- Mantiene el estado con variables.
- Se alimenta de datos y devuelve los resultados de cada operación.
Funcionamiento general¶
TensorFlow es un sistema de programación en el que representamos cálculos en forma de grafos. Los nodos en el grafo se llaman ops (abreviatura de operaciones). Una op tiene cero o más tensores, realiza algún cálculo, y produce cero o más tensores.
Un grafo de TensorFlow es una descripción de cálculos. Para calcular cualquier cosa dentro de TensorFlow, el grafo debe ser lanzado dentro de una sesión. La Sesión coloca las operaciones del grafo en los diferentes dispositivos, tales como CPU o GPU, y proporciona métodos para ejecutarlas.
Creando un Grafo¶
Para construir un grafo simple, podemos comenzar con ops que no necesitan ningún dato de entrada, como son las constantes y luego le pasamos su salida a ops que realizan cálculos.
# importamos la libreria
import tensorflow as tf
# importamos librerías adicionales
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import pandas as pd
%matplotlib inline
Constantes¶
Podemos construir ops de constantes utilizando constant, su API es bastante simple:
constant(value, dtype=None, shape=None, name='Const')
Le debemos pasar un valor, el cual puede ser cualquier tipo de tensor (un escalar, un vector, una matriz, etc) y luego opcionalmente le podemos pasar el tipo de datos, la forma y un nombre.
# Creación de Constantes
# El valor que retorna el constructor es el valor de la constante.
# creamos constantes a=2 y b=3
a = tf.constant(2)
b = tf.constant(3)
# creamos matrices de 3x3
matriz1 = tf.constant([[1, 3, 2],
[1, 0, 0],
[1, 2, 2]])
matriz2 = tf.constant([[1, 0, 5],
[7, 5, 0],
[2, 1, 1]])
# Realizamos algunos cálculos con estas constantes
suma = tf.add(a, b)
mult = tf.mul(a, b)
cubo_a = a**3
# suma de matrices
suma_mat = tf.add(matriz1, matriz2)
# producto de matrices
mult_mat = tf.matmul(matriz1, matriz2)
Sesiones¶
Ahora que ya definimos algunas ops constantes y algunos cálculos con ellas, debemos lanzar el grafo dentro de una Sesión. Para realizar esto utilizamos el objeto Session. Este objeto va a encapsular el ambiente en el que las operaciones que definimos en el grafo van a ser ejecutadas y los tensores son evaluados.
# Todo en TensorFlow ocurre dentro de una Sesión
# creamos la sesion y realizamos algunas operaciones con las constantes
# y lanzamos la sesión
with tf.Session() as sess:
print("Suma de las constantes: {}".format(sess.run(suma)))
print("Multiplicación de las constantes: {}".format(sess.run(mult)))
print("Constante elevada al cubo: {}".format(sess.run(cubo_a)))
print("Suma de matrices: \n{}".format(sess.run(suma_mat)))
print("Producto de matrices: \n{}".format(sess.run(mult_mat)))
Las Sesiones deben ser cerradas para liberar los recursos, por lo que es una buena práctica incluir la Sesión dentro de un bloque "with" que la cierra automáticamente cuando el bloque termina de ejecutar.
Para ejecutar las operaciones y evaluar los tensores utilizamos Session.run().
# Creamos una variable y la inicializamos con 0
estado = tf.Variable(0, name="contador")
# Creamos la op que le va a sumar uno a la Variable `estado`.
uno = tf.constant(1)
nuevo_valor = tf.add(estado, uno)
actualizar = tf.assign(estado, nuevo_valor)
# Las Variables deben ser inicializadas por la operación `init` luego de
# lanzar el grafo. Debemos agregar la op `init` a nuestro grafo.
init = tf.initialize_all_variables()
# Lanzamos la sesion y ejecutamos las operaciones
with tf.Session() as sess:
# Ejecutamos la op `init`
sess.run(init)
# imprimir el valor de la Variable estado.
print(sess.run(estado))
# ejecutamos la op que va a actualizar a `estado`.
for _ in range(3):
sess.run(actualizar)
print(sess.run(estado))
# Ejemplo variables simbólicas en los grafos
# El valor que devuelve el constructor representa la salida de la
# variable (la entrada de la variable se define en la sesion)
# Creamos un contenedor del tipo float. Un tensor de 4x4.
x = tf.placeholder(tf.float32, shape=(4, 4))
y = tf.matmul(x, x)
with tf.Session() as sess:
# print(sess.run(y)) # ERROR: va a fallar porque no alimentamos a x.
rand_array = np.random.rand(4, 4)
print(sess.run(y, feed_dict={x: rand_array})) # ahora esta correcto.
Ahora ya conocemos en líneas generales como es la mecánica detrás del funcionamiento de TensorFlow y como deberíamos proceder para crear las operaciones dentro de los grafos. Veamos si podemos implementar modelos de neuronas simples con la ayuda de esta librería.
Ejemplo de neuronas simples¶
Una neurona simple, va a tener una forma similar al siguiente diagrama:
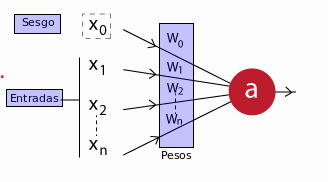
En donde sus componentes son:
$x_1, x_2, \dots, x_n$: son los datos de entrada en la neurona, los cuales también puede ser que sean producto de la salida de otra neurona de la red.
$x_0$: Es la unidad de sesgo; un valor constante que se le suma a la entrada de la función de activación de la neurona. Generalmente tiene el valor 1. Este valor va a permitir cambiar la función de activación hacia la derecha o izquierda, otorgándole más flexibilidad para aprender a la neurona.
$w_0, w_1, w_2, \dots, w_n$: Los pesos relativos de cada entrada. Tener en cuenta que incluso la unidad de sesgo tiene un peso.
a: La salida de la neurona. Que va a ser calculada de la siguiente forma:
Aquí $f$ es la función de activación de la neurona. Esta función es la que le otorga tanta flexibilidad a las redes neuronales y le permite estimar complejas relaciones no lineales en los datos. Puede ser tanto una función lineal, una función logística, hiperbólica, etc.
Ahora que ya conocemos como se construye una neurona tratemos de implementar con este modelo las funciones lógicas AND, OR y XNOR. Podemos pensar a estas funciones como un problema de clasificación en el que la salida va a ser 0 o 1, de acuerdo a la combinación de las diferentes entradas.
Las podemos modelar linealmente con la siguiente función de activación:
$$f(x) = \left\{ \begin{array}{ll} 0 & \mbox{si } x < 0 \\ 1 & \mbox{si } x \ge 0 \end{array} \right.$$Neurona AND¶
La neurona AND puede ser modelada con el siguiente esquema:
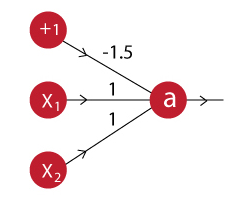
La salida de esta neurona entonces va a ser:
$$a = f(-1.5 + x_1 + x_2)$$Veamos como la podemos implementar en TensorFlow.
# Neurona con TensorFlow
# Defino las entradas
entradas = tf.placeholder("float", name='Entradas')
datos = np.array([[0, 0]
,[1, 0]
,[0, 1]
,[1, 1]])
# Defino las salidas
uno = lambda: tf.constant(1.0)
cero = lambda: tf.constant(0.0)
with tf.name_scope('Pesos'):
# Definiendo pesos y sesgo
pesos = tf.placeholder("float", name='Pesos')
sesgo = tf.placeholder("float", name='Sesgo')
with tf.name_scope('Activacion'):
# Función de activación
activacion = tf.reduce_sum(tf.add(tf.matmul(entradas, pesos), sesgo))
with tf.name_scope('Neurona'):
# Defino la neurona
def neurona():
return tf.case([(tf.less(activacion, 0.0), cero)], default=uno)
# Salida
a = neurona()
# path de logs
logs_path = '/tmp/tensorflow_logs/neurona'
# Lanzar la Sesion
with tf.Session() as sess:
# para armar el grafo
summary_writer = tf.train.SummaryWriter(logs_path,
graph=sess.graph)
# para armar tabla de verdad
x_1 = []
x_2 = []
out = []
act = []
for i in range(len(datos)):
t = datos[i].reshape(1, 2)
salida, activ = sess.run([a, activacion], feed_dict={entradas: t,
pesos:np.array([[1.],[1.]]),
sesgo: -1.5})
# armar tabla de verdad en DataFrame
x_1.append(t[0][0])
x_2.append(t[0][1])
out.append(salida)
act.append(activ)
tabla_info = np.array([x_1, x_2, act, out]).transpose()
tabla = pd.DataFrame(tabla_info,
columns=['x1', 'x2', 'f(x)', 'x1 AND x2'])
tabla
Aquí podemos ver los datos de entrada de $x_1$ y $x_2$, el resultado de la función de activación y la decisión final que toma la neurona de acuerdo este último resultado. Como podemos ver en la tabla de verdad, la neurona nos dice que $x_1$ and $x_2$ solo es verdad cuando ambos son verdaderos, lo que es correcto.
Neurona OR¶
La neurona OR puede ser modelada con el siguiente esquema:
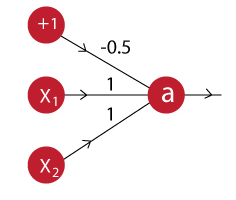
La salida de esta neurona entonces va a ser:
$$a = f(-0.5 + x_1 + x_2)$$Como se puede ver a simple vista, el modelo de esta neurona es similar a la de la neurona AND, con el único cambio en el valor del sesgo, por lo tanto solo tendríamos que cambiar ese valor en nuestro modelo anterior para crear esta nueva neurona.
# Neurona OR, solo cambiamos el valor del sesgo
with tf.Session() as sess:
# para armar el grafo
summary_writer = tf.train.SummaryWriter(logs_path,
graph=sess.graph)
# para armar tabla de verdad
x_1 = []
x_2 = []
out = []
act = []
for i in range(len(datos)):
t = datos[i].reshape(1, 2)
salida, activ = sess.run([a, activacion], feed_dict={entradas: t,
pesos:np.array([[1.],[1.]]),
sesgo: -0.5}) # sesgo ahora -0.5
# armar tabla de verdad en DataFrame
x_1.append(t[0][0])
x_2.append(t[0][1])
out.append(salida)
act.append(activ)
tabla_info = np.array([x_1, x_2, act, out]).transpose()
tabla = pd.DataFrame(tabla_info,
columns=['x1', 'x2', 'f(x)', 'x1 OR x2'])
tabla
Como vemos, cambiando simplemente el peso del sesgo, convertimos a nuestra neurona AND en una neurona OR. Como muestra la tabla de verdad, el único caso en que $x_1$ OR $x_2$ es falso es cuando ambos son falsos.
Red Neuronal XNOR¶
El caso de la función XNOR, ya es más complicado y no puede modelarse utilizando una sola neurona como hicimos con los ejemplos anteriores. $x_1$ XNOR $x_2$ va a ser verdadero cuando ambos son verdaderos o ambos son falsos, para implementar esta función lógica debemos crear una red con dos capas, la primer capa tendrá dos neuronas cuya salida servirá de entrada para una nueva neurona que nos dará el resultado final. Esta red la podemos modelar de acuerdo al siguiente esquema:
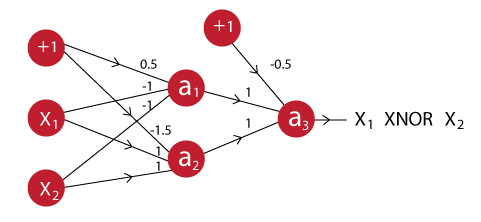
Veamos entonces si podemos implementar este modelo en TensorFlow.
# Red Neuronal XNOR con TensorFlow
# Defino las entradas
entradas = tf.placeholder("float", name='Entradas')
datos = np.array([[0, 0]
,[1, 0]
,[0, 1]
,[1, 1]])
# Defino las salidas
uno = lambda: tf.constant(1.0)
cero = lambda: tf.constant(0.0)
with tf.name_scope('Pesos'):
# Definiendo pesos y sesgo
pesos = {
'a1': tf.constant([[-1.0], [-1.0]], name='peso_a1'),
'a2': tf.constant([[1.0], [1.0]], name='peso_a2'),
'a3': tf.constant([[1.0], [1.0]], name='peso_a3')
}
sesgo = {
'a1': tf.constant(0.5, name='sesgo_a1'),
'a2': tf.constant(-1.5, name='sesgo_a2'),
'a3': tf.constant(-0.5, name='sesgo_a3')
}
with tf.name_scope('Red_neuronal'):
# Defino las capas
def capa1(entradas, pesos, sesgo):
# activacion a1
a1 = tf.reduce_sum(tf.add(tf.matmul(entradas, pesos['a1']), sesgo['a1']))
a1 = tf.case([(tf.less(a1, 0.0), cero)], default=uno)
# activacion a2
a2 = tf.reduce_sum(tf.add(tf.matmul(entradas, pesos['a2']), sesgo['a2']))
a2 = tf.case([(tf.less(a2, 0.0), cero)], default=uno)
return a1, a2
def capa2(entradas, pesos, sesgo):
# activacion a3
a3 = tf.reduce_sum(tf.add(tf.matmul(entradas, pesos['a3']), sesgo['a3']))
a3 = tf.case([(tf.less(a3, 0.0), cero)], default=uno)
return a3
# path de logs
logs_path = '/tmp/tensorflow_logs/redXNOR'
# Sesion red neuronal XNOR
with tf.Session() as sess:
# para armar el grafo
summary_writer = tf.train.SummaryWriter(logs_path,
graph=sess.graph)
# para armar tabla de verdad
x_1 = []
x_2 = []
out = []
for i in range(len(datos)):
t = datos[i].reshape(1, 2)
# obtenos resultados 1ra capa
a1, a2 = sess.run(capa1(entradas, pesos, sesgo), feed_dict={entradas: t})
# pasamos resultados a la 2da capa
ent_a3 = np.array([[a1, a2]])
salida = sess.run(capa2(ent_a3, pesos, sesgo))
# armar tabla de verdad en DataFrame
x_1.append(t[0][0])
x_2.append(t[0][1])
out.append(salida)
tabla_info = np.array([x_1, x_2, out]).transpose()
tabla = pd.DataFrame(tabla_info,
columns=['x1', 'x2', 'x1 XNOR x2'])
tabla
Como vemos, la red neuronal nos da el resultado correcto para la función lógica XNOR, solo es verdadera si ambos valores son verdaderos, o ambos son falsos.
Hasta aquí implementamos simples neuronas y les pasamos los valores de sus pesos y sesgo a mano; esto es sencillo para los ejemplos; pero en la vida real, si queremos utilizar redes neuronales necesitamos implementar un procesos que vaya actualizando los pesos a medida que la red vaya aprendiendo con el entrenamiento. Este proceso se conoce con el nombre de propagación hacia atrás o backpropagation.
Propagación hacia atrás¶
La propagación hacia atrás o backpropagation es un algoritmo que funciona mediante la determinación de la pérdida (o error) en la salida y luego propagándolo de nuevo hacia atrás en la red. De esta forma los pesos se van actualizando para minimizar el error resultante de cada neurona. Este algoritmo es lo que les permite a las redes neuronales aprender.
Veamos un ejemplo de como podemos implementar una red neuronal que pueda aprender por sí sola con la ayuda de TensorFlow.
Ejemplo de Perceptron multicapa para reconocer dígitos escritos¶
En este ejemplo vamos a construir un peceptron multicapa para clasificar dígitos escritos. Antes de pasar a la construcción del modelo, exploremos un poco el conjunto de datos con el que vamos a trabajar en la clasificación.
MNIST dataset¶
MNIST es un simple conjunto de datos para reconocimiento de imágenes por computadora. Se compone de imágenes de dígitos escritos a mano como los siguientes:

Para más información sobre el dataset pueden visitar el siguiente enlace, en donde hacen un análisis detallado del mismo.
# importando el dataset
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
Explorando MNIST dataset¶
# forma del dataset 55000 imagenes
mnist.train.images.shape
# cada imagen es un array de 28x28 con cada pixel
# definido como escala de grises.
digito1 = mnist.train.images[0].reshape((28, 28))
# visualizando el primer digito
plt.imshow(digito1, cmap = cm.Greys)
plt.show()
# valor correcto
mnist.train.labels[0].nonzero()[0][0]
# visualizando imagenes de 5 en 5
def visualizar_imagenes(dataset, cant_img):
img_linea = 5
lineas = int(cant_img / img_linea)
imagenes = []
for i in range(lineas):
datos = []
for img in dataset[img_linea* i:img_linea* (i+1)]:
datos.append(img.reshape((28,28)))
imgs = np.hstack(datos)
imagenes.append(imgs)
data = np.vstack(imagenes)
plt.imshow(data, cmap = cm.Greys )
plt.show()
# visualizando los primeros 30 dígitos
plt.figure(figsize=(8, 8))
visualizar_imagenes(mnist.train.images, 30)
Construyendo el perceptron multicapa¶
Ahora que ya conocemos los datos con los que vamos a trabajar, ya estamos en condiciones de construir el modelo. Vamos a construir un peceptron multicapa que es una de las redes neuronales más simples. El modelo va a tener dos capas ocultas, que se van a activar con la función de activación ReLU y vamos a optimizar los pesos reduciendo la entropía cruzada utilizando el algoritmo Adam que es un método para optimización estocástica.
# Parametros
tasa_aprendizaje = 0.001
epocas = 15
lote = 100
display_step = 1
logs_path = "/tmp/tensorflow_logs/perceptron"
# Parametros de la red
n_oculta_1 = 256 # 1ra capa de atributos
n_oculta_2 = 256 # 2ra capa de atributos
n_entradas = 784 # datos de MNIST(forma img: 28*28)
n_clases = 10 # Total de clases a clasificar (0-9 digitos)
# input para los grafos
x = tf.placeholder("float", [None, n_entradas], name='DatosEntrada')
y = tf.placeholder("float", [None, n_clases], name='Clases')
# Creamos el modelo
def perceptron_multicapa(x, pesos, sesgo):
# Función de activación de la capa escondida
capa_1 = tf.add(tf.matmul(x, pesos['h1']), sesgo['b1'])
# activacion relu
capa_1 = tf.nn.relu(capa_1)
# Función de activación de la capa escondida
capa_2 = tf.add(tf.matmul(capa_1, pesos['h2']), sesgo['b2'])
# activación relu
capa_2 = tf.nn.relu(capa_2)
# Salida con activación lineal
salida = tf.matmul(capa_2, pesos['out']) + sesgo['out']
return salida
# Definimos los pesos y sesgo de cada capa.
pesos = {
'h1': tf.Variable(tf.random_normal([n_entradas, n_oculta_1])),
'h2': tf.Variable(tf.random_normal([n_oculta_1, n_oculta_2])),
'out': tf.Variable(tf.random_normal([n_oculta_2, n_clases]))
}
sesgo = {
'b1': tf.Variable(tf.random_normal([n_oculta_1])),
'b2': tf.Variable(tf.random_normal([n_oculta_2])),
'out': tf.Variable(tf.random_normal([n_clases]))
}
with tf.name_scope('Modelo'):
# Construimos el modelo
pred = perceptron_multicapa(x, pesos, sesgo)
with tf.name_scope('Costo'):
# Definimos la funcion de costo
costo = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, y))
with tf.name_scope('optimizador'):
# Algoritmo de optimización
optimizar = tf.train.AdamOptimizer(
learning_rate=tasa_aprendizaje).minimize(costo)
with tf.name_scope('Precision'):
# Evaluar el modelo
pred_correcta = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
# Calcular la precisión
Precision = tf.reduce_mean(tf.cast(pred_correcta, "float"))
# Inicializamos todas las variables
init = tf.initialize_all_variables()
# Crear sumarización para controlar el costo
tf.scalar_summary("Costo", costo)
# Crear sumarización para controlar la precisión
tf.scalar_summary("Precision", Precision)
# Juntar los resumenes en una sola operación
merged_summary_op = tf.merge_all_summaries()
# Lanzamos la sesión
with tf.Session() as sess:
sess.run(init)
# op to write logs to Tensorboard
summary_writer = tf.train.SummaryWriter(
logs_path, graph=tf.get_default_graph())
# Entrenamiento
for epoca in range(epocas):
avg_cost = 0.
lote_total = int(mnist.train.num_examples/lote)
for i in range(lote_total):
lote_x, lote_y = mnist.train.next_batch(lote)
# Optimización por backprop y funcion de costo
_, c, summary = sess.run([optimizar, costo, merged_summary_op],
feed_dict={x: lote_x, y: lote_y})
# escribir logs en cada iteracion
summary_writer.add_summary(summary, epoca * lote_total + i)
# perdida promedio
avg_cost += c / lote_total
# imprimir información de entrenamiento
if epoca % display_step == 0:
print("Iteración: {0: 04d} costo = {1:.9f}".format(epoca+1,
avg_cost))
print("Optimización Terminada!\n")
print("Precisión: {0:.2f}".format(Precision.eval({x: mnist.test.images,
y: mnist.test.labels})))
print("Ejecutar el comando:\n",
"--> tensorboard --logdir=/tmp/tensorflow_logs ",
"\nLuego abir https://0.0.0.0:6006/ en el navegador")
Como vemos TensorFlow nos da mucha flexibilidad para construir el modelo, modificando muy pocas líneas podríamos cambiar el algoritmo de optimización o el calculo del error y obtener otros resultados; de esta forma vamos a poder personalizar el modelo para alcanzar mayores niveles de precisión.
TensorBoard¶
Otra gran herramienta que nos proporciona TensorFlow es TensorBoard que nos permite visualizar nuestros grafos y nos ayudan a alcanzar un mayor entendimiento del flujo de cálculos que ocurre en nuestro modelo.
Para crear la información de la que se va a nutrir el TensorBoard, podemos definir algunos scopes utilizando tf.name_scope; también podemos incluir algunos gráficos sumarizados con tf.scalar_summary y luego llamamos a la función tf.train.SummaryWriter dentro de una Sesión.
Luego podemos iniciar el board con el comando tensorboard --logdir=logpath como se puede ver en la salida del último ejemplo.
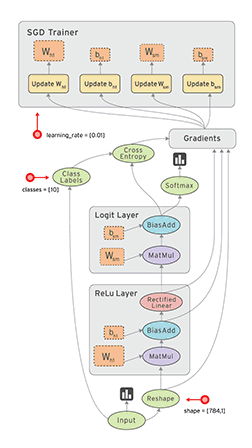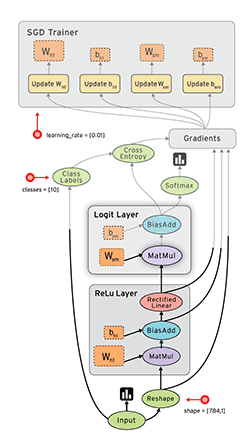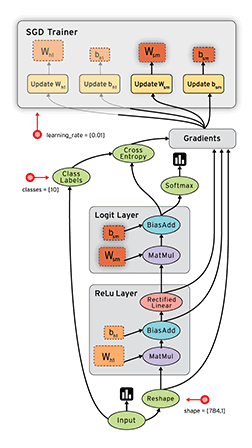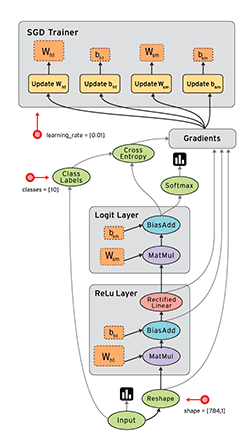
Los grafos de los casos que vimos por ejemplo, se ven así.
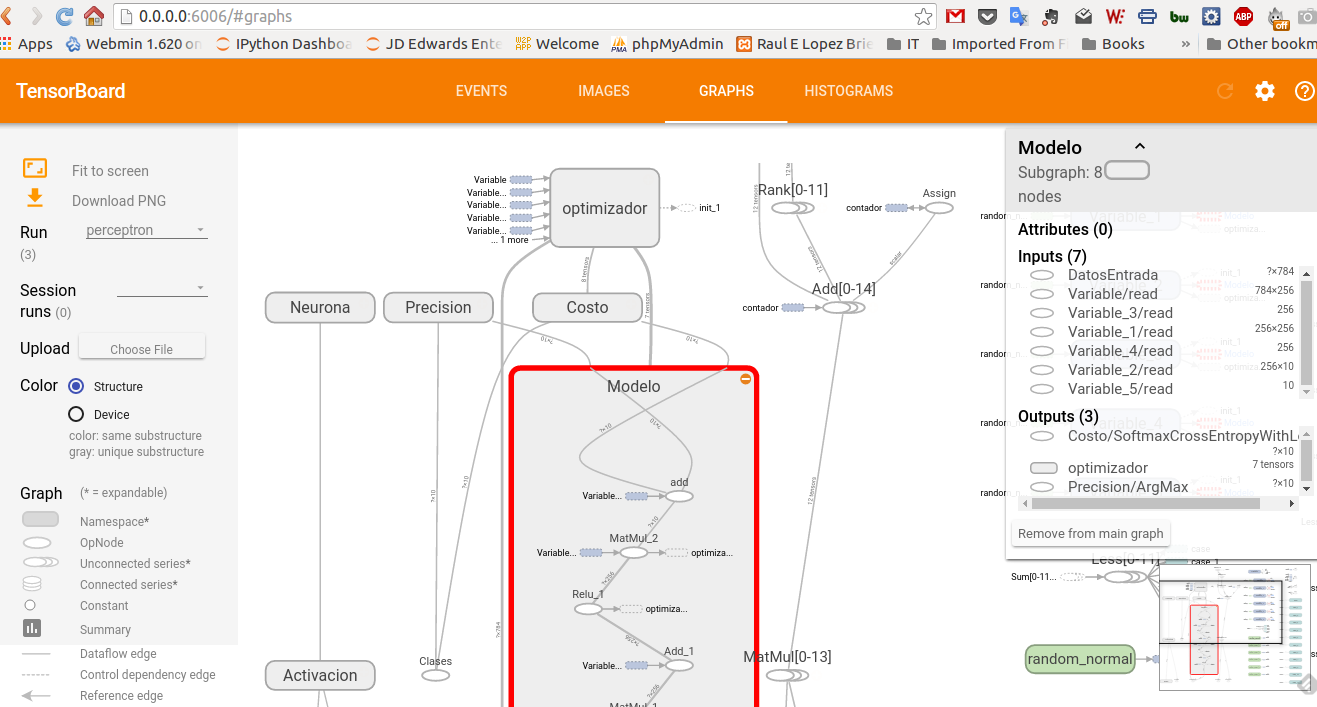
Los invito a explorar la herramienta y adentrarse en el fascinante mundo de las redes neuronales.
Saludos!